リスト処理による積集合

前述の方法は、リストに含まれる/含まれないを、2進数の0/1で表現する方式である。しかし、2進数であれば、int で 31要素、long int で 63 要素が上限となってしまう。

しかし、リスト構造であれば、リストの要素として扱うことで、要素件数は自由に扱える。また、今までの授業で説明してきた cons() などを使って表現すれば、簡単なプログラムでリストの処理が記述できる。

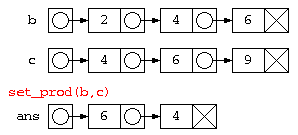
例えば、積集合(a ∩ b)を求めるのであれば、リストa の各要素が、リストb の中に含まれるか find 関数でチェックし、 両方に含まれたものだけを、ans に加えていく…という考えでプログラムを作ると以下のようになる。

import java.util.*;

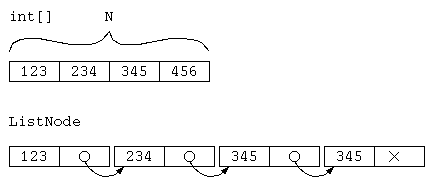
class ListNode {
   int      data ;
   ListNode next ;
   ListNode( int d , ListNode n ) {
       this.data = d ;
       this.next = n ;
   }
   static void print( ListNode p ) {
      for( ; p != null ; p = p.next )
         System.out.print( p.data + " " ) ;
      System.out.println() ;
   }
   static boolean find( ListNode p , int key ) {
      for( ; p != null ; p = p.next )
         if ( p.data == key )
            return true ;
      return false ;
   }
   static ListNode set_prod( ListNode a , ListNode b ) {
      ListNode ans = null ;
      for( ; a != null ; a = a.next ) {
         if ( find( b , a.data ) )
            ans = new ListNode( a.data , ans ) ;
      }
      return ans ;
   }
} ;

public class Main {
    public static void main(String[] args) throws Exception {
        ListNode b = new ListNode( 2 , new ListNode( 4 , new ListNode( 6 , null ) ) ) ;
        ListNode c = new ListNode( 4 , new ListNode( 6 , new ListNode( 9 , null ) ) ) ;
        ListNode b_and_c = ListNode.set_prod( b , c ) ;
        ListNode.print( b_and_c ) ;
    }
}

例題として、和集合、差集合などを考えてみよう。

理解確認

• 2進数を用いた集合処理は、どのように行うか？
• リスト構造を用いた集合処理は、どのように行うか？
• 積集合(A ∩ B)、和集合(A ∪ B)、差集合(A – B) の処理を記述せよ。

---

リスト構造の利点と欠点

リストを使った集合演算のように、データを連ねたリストは、単純リストとか線形リストと呼ばれる。特徴はデータ数に応じてメモリを確保する点や、途中へのデータの挿入削除が得意な点があげられる。一方で、配列は想定最大データ件数で宣言してしまうと、実際のデータ数が少ない場合、メモリの無駄も発生する。しかし、想定件数と実データ件数がそれなりに一致していれば、無駄も必要最小限となる。リスト構造では、次のデータへのポインタを必要とすることから、常にポインタ分のメモリは、データにのみ注目すれば無駄となる。

例えば、整数型のデータを最大 MAX 件保存したいけど、実際は それ以下の、平均 N 件扱うとする。この時のメモリの使用量 M は、以下のようになるであろう。(sizeof()はC言語での指定した型のメモリByte数を返す演算子)

配列の場合	リスト構造の場合
	(ただしヒープ管理用メモリ使用量は無視)

シーケンシャルアクセス・ランダムアクセス

もう１つのリストの欠点はシーケンシャルアクセス。テープ上に記録された情報を読む場合、後ろのデータを読むには途中データを読み飛ばす必要があり、データ件数に比例したアクセス時間を要する。このような N番目 データ参照に、O(N )の時間を要するものは、シーケンシャルアクセスと呼ばれる。

一方、配列はどの場所であれ、一定時間でデータの参照が可能であり、これは ランダムアクセスと呼ばれる。N番目のアクセス時間がO(1 )を要する。配列であれば、N/2 番目のデータをO(1)で簡単に取り出せるから2分探索法が有効だが、リスト構造であれば、N/2番目のデータを取り出すのにO(N )かかってしまう。

このため、プログラム・エディタの文字データの管理などに単純リストを用いた場合、１つ前の行に移動するには、先頭から編集行までの移動で O(N ) の時間がかかり、大量の行数の編集では、使いものにならない。ここで、シーケンシャルアクセスでも１つ前にもどるだけでも処理時間を改善してみよう。