コンピュータとN進数
3年の情報制御基礎の授業の一回目。この授業では、情報系以外の学生も受講することから、基礎的な共通的な話題を中心に説明を行う。
情報制御基礎のシラバス
情報制御基礎では、ここに上げたシラバス(2023)に沿って授業を行う。
基本的に、センサーから読み取ったデータを使って動く制御系システムを作る場合の基礎知識ということで、アナログ量・デジタル量の話から、移動平均やデータ差分といった数値処理や、そこで求まった値を制御に用いるための基礎的な話を行う。
コンピュータと組み込み系
最近では、コンピュータといっても様々な所で使われている。
- 科学技術計算用の大型コンピュータ(最近なら富岳や京が有名)や
- インターネットの処理を行うサーバ群
(必要に応じてサービスとして提供されるものはクラウドコンピューティングと呼ぶ)、 - デスクトップパソコン・ノートパソコン
- タブレットPCやスマートフォンのような端末、
- 電化製品の中に収まるようなワンチップコンピュータ
などがある。(3)のパソコンでもグラフィックス表示機能のために GPU(Graphics Processing Unit) を搭載したものは(ゲームでの3次元表示用)、高速計算に使われることも多い。

(5) ワンチップコンピュータ:PIC
身近で使われている情報制御という点では、(5)のような小型のコンピュータも多く、こういったものは組み込み型コンピュータとも呼ばれる。しかし、こういったコンピュータは、小さく機能も限られているので、
- 組み込み系では、扱える数値が整数で 8bit や 16bit といった精度しかなかったり、
- 実数を伴う複雑な計算をするには、処理時間がかかったりする
ため、注意が必要である。
この情報制御基礎の授業では、組み込み系のコンピュータでも数値を正しく扱うための知識や、こういった小さいコンピュータで制御を行うことを踏まえたプログラミングの基礎となる知識を中心に説明を行う。
2進数と10進数
コンピュータの中では、電圧が高い/低いといった状態で0と1の2通りの状態を表し、その 0/1 を組み合わせて、大きな数字を表す(2進数)。
練習として、2進数を10進数で表したり、10進数を2進数に直してみよう。
N進数を10進数に変換
N進数で “abcde” があったとする。(2進数で”10101)2“とか、10進数で”12345)10“とか)
この値は、以下のような式で表せる。
(例1)
(例2)
10進数をN進数に変換
N進数のは、前式を変形すると、以下のような式で表せることから、
値をNで割った余りを求めると、N進数の最下位桁eを取り出せる。
このため、10進数で与えられた35を2進数に変換するのであれば、35を2で次々と割った余りを、下の桁から書きならべれば2進数100011)2が得られる。
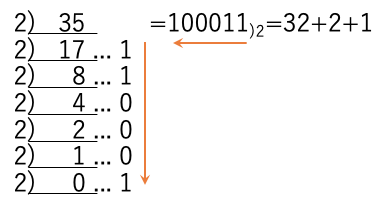
実数の場合
途中に小数点を含むN進数のab.cde)Nであれば、以下の値を意味する。
ここで、小数点以下だけを取り出した、0.cde)Nを考えると、
の値に、Nをかけると、次のように変形できる。
この式を見ると、小数部にNをかけると、整数部分に小数点以下1桁目が取り出せる。
このため、10進数で与えられた、0.625を2進数に変換するのであれば、0.625に次々と2をかけて、その整数部を上の桁から書きならべれば、2進数0.101)2が得られる。
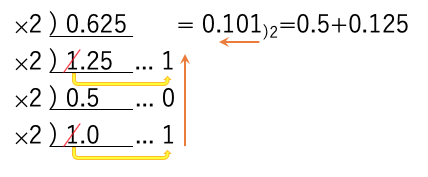
ただし、10進数で0.1という値で、上記の計算を行うと、延々と繰り返しが発生する。つまり、無限小数になるので注意せよ。
2の補数と負の数
コンピュータの中で引き算を行う場合には、2の補数がよく使われる。2の補数とは、2進数の0と1を入替えた結果(1の補数)に、1を加えた数である。

元の数に2の補数
を加えると(2進数が8bitの数であれば)、どのような数でも1,0000,0000という値になる。この先頭の9bit目が必ずはみ出し、この値を覚えないのであれば、元の数+2の補数=0とみなすことができる。このことから、2の補数= (-元の数) であり、負の数を扱うのに都合が良い。
練習問題
(1) 自分の誕生日で、整数部を誕生日の日、小数点以下を誕生日の月とした値について、2進数に変換せよ。(例えば、2月7日の場合は、”7.02″という小数点を含む10進数とする。)
変換の際には、上の説明の中にあるような計算手順を示すこと。また、その2進数を10進数に直し、元の値と同じか確認すること。(ただし、結果の2進数が無限小数になる場合最大7桁まで求めれば良い。同じ値か確認する際には無限少数の場合は近い値になるか確認すること)
(2) 自分の誕生日の日と、自分の学籍番号の下2桁の値を加えた値について、8bitの2進数で表わせ。(2月7日生まれの出席番号13番なら7+13=21)
その後、8bitの2進数として、2の補数を求めよ。また、元の数と2の補数を加えた値についても検証すること。
レポートの提出先は、こちらのリンクを参照(この中にレポート書式のひな型を置いてあります)
複素数クラスによる演習
複素数クラスの例
隠蔽化と基本的なオブジェクト指向の練習課題として、前回の授業では、直交座標系による複素数クラスを示した。今回の授業では、演習を行うとともに直交座標系を極座標系にクラス内部を変更したことにより、隠蔽化の効果について考えてもらい、第1回レポートとする。
直交座標系
前回の授業で示した直交座標系のクラス。比較対象とするために再掲。
#include <stdio.h>
#include <math.h>
// 直交座標系の複素数クラス
class Complex {
private:
double re ; // 実部
double im ; // 虚部
public:
void print() {
printf( "%lf + j%lf¥n" , re , im ) ;
}
Complex( double r , double i ) // 実部虚部のコンストラクタ
: re( r ) , im( i ) {}
Complex() // デフォルトコンストラクタ
: re( 0.0 ) , im( 0.0 ) {}
void add( Complex z ) {
// 加算は、直交座標系だと極めてシンプル
re = re + z.re ;
im = im + z.im ;
}
void mul( Complex z ) {
// 乗算は、直交座標系だと、ちょっと煩雑
double r = re * z.re - im * z.im ;
double i = re * z.im + im * z.re ;
re = r ;
im = i ;
}
double get_re() {
return re ;
}
double get_im() {
return im ;
}
double get_abs() { // 絶対値
return sqrt( re*re + im*im ) ;
}
double get_arg() { // 偏角
return atan2( im , re ) ;
}
} ; // ←何度も繰り返すけど、ここのセミコロン忘れないでね
int main() {
// 複素数を作る
Complex a( 1.0 , 2.0 ) ;
Complex b( 2.0 , 3.0 ) ;
// 複素数の計算
a.print() ;
a.add( b ) ;
a.print() ;
a.mul( b ) ;
a.print() ;
return 0 ;
}
極座標系
上記の直交座標系の Complex クラスは、加減算の関数は単純だけど、乗除算の関数を書く時には面倒になってくる。この場合、極座標系でプログラムを書いたほうが判りやすいかもしれない。
// 局座標系の複素数クラス
class Complex {
private:
double r ; // 絶対値 r
double th ; // 偏角 θ
public:
void print() {
printf( "%lf ∠ %lf¥n" , r , th / 3.14159265 * 180.0 ) ;
}
Complex() // デフォルトコンストラクタ
: r( 0.0 ) , th( 0.0 ) {}
// 表面的には、同じ使い方ができるように
// 直交座標系でのコンストラクタ
Complex( double x , double y ) {
r = sqrt( x*x + y*y ) ;
th = atan2( y , x ) ; // 象限を考慮したatan()
}
// 極座標系だと、わかりやすい処理
void mul( Complex z ) {
// 極座標系での乗算は
r = r * z.r ; // 絶対値の積
th = th + z.th ; // 偏角の和
}
// 反対に、加算は面倒な処理になってしまう。
void add( Complex z ) {
; // 自分で考えて
}
// ゲッターメソッド
double get_abs() {
return r ;
}
double get_arg() {
return th ;
}
double get_re() { // 直交座標系との互換性のためのゲッターメソッド
return r * cos( th ) ;
}
double get_im() {
return r * sin( th ) ;
}
} ; // ←しつこく繰り返すけど、セミコロン忘れないでね(^_^;
このように、プログラムを開発していると、当初は直交座標系でプログラムを記述していたが、途中で極座標系の方がプログラムが書きやすいという局面となるかもしれない。しかし、オブジェクト指向による隠蔽化を正しく行っていれば、利用者に影響なく「データ構造」や「その手続き(メソッド)」を書換えることも可能となる。
このように、プログラムをさらに良いものとなるべく書換えることは、オブジェクト指向ではリファクタリングと呼ぶ。
正しくクラスを作っていれば、クラス利用者への影響が最小にしながらリファクタリングが可能となる。
const 指定 (経験者向け解説)
C++ では、間違って値を書き換えるような処理を書けないようにするための、const 指定の機能がある。
void bar( char* s ) { // void bar( const char* s ) {...}
printf( "%s\n" , s ) ; // で宣言すべき。
}
void foo( const int x ) {
// ~~~~~~~~~~~
x++ ; // 定数を書き換えることはできない。
printf( "%d\n" , x ) ;
}
int main() {
const double pi = 3.141592 ;
// C言語で #define PI 3.141592 と同等
bar( "This is a pen" ) ; // Warning: string constant to 'char*' の警告
int a = 123 ;
foo( a ) ;
return 0 ;
}
前述の、getter メソッドの例では要素を参照するだけで、オブジェクトの中身が変化しない。逆に言えば、getter のメソッド内にはオブジェクトに副作用のある処理を書いてはいけない。こういった用途に、オブジェクトを変化させないメソッド宣言がある。先の、get_re() は、
class ... {
:
inline double get_re() const {
// ~~~~~
re = 0 ; // 文法エラー
return re ;
}
} ;
クラスオブジェクトを引数にする場合
前述の add() メソッドでは、”void add( Complex z ) { … }” にて宣言をしていた。しかし、引数となる変数 z の実体が巨大な場合、この書き方では値渡しになるため、データの複製の処理時間が問題となる場合がある。この場合は、(書き方1)のように、z の参照渡しにすることで、データ複製の時間を軽減する。また、この例では、引数 z の中身を間違って add() の中で変化させる処理を書いてしまうかもしれない。そこで、この事例では(書き方2)のように const 指定もすべきである。
// (書き方1)
class Complex {
:
void add( Complex& z ) {
re += z.re ;
im += z.im ;
}
} ;
// (書き方2)
class Complex {
:
void add( const Complex& z )
{ // ~~~~~~~~~~~~~~~~
re += z.re ;
im += z.im ;
}
} ;
レポート1(複素数の加減乗除)
授業中に示した、直交座標系・極座標系の複素数のプログラムをベースに、記載されていない減算・除算のプログラムを作成し、レポートを作成する。 レポートには、下記のものを記載すること。
- プログラムリスト
- プログラムへの説明
- 動作確認の結果
- プログラムより理解できること。
- 実際にプログラムを書いてみて分かった問題点など…
オブジェクト指向の基本プログラムと複素数クラス
C++のクラスで表現
前回の講義での、構造体のポインタ渡しをC++の基本的なクラスで記述した場合のプログラムを再掲する。
#include <stdio.h>
#include <string.h>
// この部分はクラス設計者が書く
class Person {
private: // クラス外からアクセスできない部分
// データ構造を記述
char name[10] ; // メンバーの宣言
int age ;
public: // クラス外から使える部分
// データに対する処理を記述
void set( char s[] , int a ) { // メソッドの宣言
// pのように対象のオブジェクトを明記する必要はない。
strcpy( name , s ) ;
age = a ;
}
void print() {
printf( "%s %d¥n" , name , age ) ;
}
} ; // ← 注意ここのセミコロンを書き忘れないこと。
// この部分はクラス利用者が書く
int main() {
Person saitoh ;
saitoh.set( "saitoh" , 55 ) ;
saitoh.print() ;
// 文法エラーの例
printf( "%d¥n" , saitoh.age ) ; // phoneはprivateなので参照できない。
return 0 ;
}
この様にC++のプログラムに書き換えたが、内部の処理は元のC言語と同じであり、オブジェクトへの関数呼び出し saitoh.set(…) などが呼び出されても、set() は、オブジェクトのポインタを引数して持つ関数として、機械語が生成されるだけである。
用語の解説:C++のプログラムでは、データ構造とデータの処理を、並行しながら記述する。 データ構造に対する処理は、メソッド(method)と呼ばれる。 データ構造とメソッドを同時に記載したものは、クラス(class)と呼ぶ。 そのデータに対し具体的な値や記憶域が割り当てられたものをオブジェクト(object)と呼ぶ。
C++では隠蔽化をさらに明確にするために、private: や public: といったアクセス制限を指定できる。private: は、そのメソッドの中でしか使うことができない要素や関数であり、public: は、メソッド以外からでも参照したり呼出したりできる。オブジェクト指向でプログラムを書くとき、データ構造や関数の処理方法は、クラス内部の設計者しか触れないようにしておけば、その内部を改良することができる。しかし、クラスの利用者が勝手に内部データを触っていると、内部設計者が改良するとそのプログラムは動かないものになってしまう。
隠蔽化を的確に行うことで、クラスの利用者はクラスの内部構造を触ることができなくなる。一方でクラス設計者はクラスの外部への挙動が変化しないようにクラス内部を修正することに心がければ、クラス利用者への影響がないままクラスの内部を改良できる。このように利用者への影響を最小に、常にプログラムを修正することをリファクタリングと呼ぶ。
クラス限定子
前述のプログラムでは、class 宣言の中に関数内部の処理を記述していた。しかし関数の記述が長い場合は、書ききれないこういう場合はクラス限定子を使って、メソッドの具体的な処理をクラス宣言の外に記載する。
class Person {
private:
char name[10] ;
int age ;
public:
// メソッドのプロトタイプ宣言
void set( char s[] , int a) ;
void print() ;
} ;
// メソッドの実体をクラス宣言の外に記載する。
void Person::set( char s[] , int a ) { // Person::set()
strcpy( name , s ) ;
age = a ;
}
void Person::print() { // Person::print()
printf( "%s %d¥n" , name , age ) ;
}
inline 関数と開いたサブルーチン
オブジェクト指向では、きわめて簡単な処理な関数を使うことも多い。
例えば、上記のプログラム例で、クラス利用者に年齢を読み出すことは許しても書き込みをさせたくない場合、以下のような、inline 関数を定義する。(getterメソッド)
# 逆に、値の代入専用のメソッドは、setterメソッドと呼ぶclass Person { private: char name[10] ; int age ; public: // メソッドのプロトタイプ宣言 inline int get_age() { return age ; } // getter inline void set_age( int a ) { age = a ; } // setter } ;ここで inline とは、開いた関数(開いたサブルーチン)を作る指定子である。通常、機械語を生成するとき中身を参照するだけの機械語と、get_age() を呼出したときに関数呼び出しを行う機械語が作られる(閉じたサブルーチン)が、age を参照するだけのために関数呼び出しの機械語はムダが多い。inline を指定すると、入り口出口のある関数は生成されず、get_age() の処理にふさわしい age を参照するだけの機械語が生成される。
# 質問:C言語で開いたサブルーチンを使うためにはどういった機能があるか?
コンストラクタとデストラクタ
プログラムを記述する際、データの初期化忘れや終了処理忘れで、プログラムの誤動作の原因になることが多い。
このための機能がコンストラクタ(構築子)とデストラクタ(破壊子)という。
コンストラクタは、返り値を記載しない関数でクラス名(仮引数…)の形式で宣言し、オブジェクトの宣言時に初期化を行う処理として呼び出される。デストラクタは、~クラス名() の形式で宣言し、オブジェクトが不要となる際に、自動的に呼び出し処理が埋め込まれる。
class Person {
private:
// データ構造を記述
char name[10] ;
int age ;
public:
Person() { // (A) 引数なしのコンストラクタ
name[0] = 'class Person {
private:
// データ構造を記述
char name[10] ;
int age ;
public:
Person() { // (A) 引数なしのコンストラクタ
name[0] = '\0' ;
age = 0 ;
}
Person( char s[] , int a ) { // (B) 引数ありのコンストラクタ
strcpy( name , s ) ;
age = a ;
}
~Person() { // デストラクタ
print() ;
}
void print() {
printf( "'%s' = %d¥n" , name , age ) ;
}
} ;
int main() {
Person saitoh( "saitoh" , 55 ) ; // オブジェクトsaitohを"saitoh"と55で初期化
Person tomoko ; // 引数なしのコンストラクタで初期化される。
return 0 ;
// main を抜ける時にオブジェクトsaitohは不要になるので、
// デストラクタが自動的に呼び出され、'saitoh' = 55 が表示。
// 同様に tomoko のデストラクタでは、'' = 0 を表示。
}
' ;
age = 0 ;
}
Person( char s[] , int a ) { // (B) 引数ありのコンストラクタ
strcpy( name , s ) ;
age = a ;
}
~Person() { // デストラクタ
print() ;
}
void print() {
printf( "'%s' = %d¥n" , name , age ) ;
}
} ;
int main() {
Person saitoh( "saitoh" , 55 ) ; // オブジェクトsaitohを"saitoh"と55で初期化
Person tomoko ; // 引数なしのコンストラクタで初期化される。
return 0 ;
// main を抜ける時にオブジェクトsaitohは不要になるので、
// デストラクタが自動的に呼び出され、'saitoh' = 55 が表示。
// 同様に tomoko のデストラクタでは、'' = 0 を表示。
}
このクラスの中には、(A)引数無しのコンストラクタと、(B)引数ありのコンストラクタが出てくる。C++では、同じ名前の関数でも引数の数や型に応じて呼出す関数を適切に選んでくれる。(関数のオーバーロード)
デストラクタは、データが不要となった時に自動的に呼び出してくれる関数で、一般的にはC言語でのファイルの fopen() , fclose() のようなものを使う処理で、コンストラクタで fopen() , デストラクタで fclose() を呼出すように使うことが多いだろう。同じように、コンストラクタで malloc() を呼出し、デストラクタで free() を呼出すというのが定番の使い方だろう。
複素数クラスの例
隠蔽化と基本的なオブジェクト指向の練習課題として、複素数クラスをあげる。ここでは、複素数の加算・乗算を例に説明をするので、減算・除算などの処理を記述することで、クラスの扱いに慣れてもらう。
直交座標系の複素数クラス
#include <stdio.h>
#include <math.h>
// 直交座標系の複素数クラス
class Complex {
private:
double re ; // 実部
double im ; // 虚部
public:
void print() {
printf( "%lf + j%lf¥n" , re , im ) ;
}
Complex( double r , double i ) // コンストラクタで要素の
: re( r ) , im( i ) { // 初期化はこのように書いてもいい
} // re = r ; im = i ; の意味
Complex() // デフォルトコンストラクタ
: re( 0.0 ) , im( 0.0 ) {
}
void add( Complex z ) {
// 加算は、直交座標系だと極めてシンプル
re = re + z.re ;
im = im + z.im ;
}
void mul( Complex z ) {
// 乗算は、直交座標系だと、ちょっと煩雑
double r = re * z.re - im * z.im ;
double i = re * z.im + im * z.re ;
re = r ;
im = i ;
}
double get_re() {
return re ;
}
double get_im() {
return im ;
}
double get_abs() { // 絶対値
return sqrt( re*re + im*im ) ;
}
double get_arg() { // 偏角
return atan2( im , re ) ;
}
} ; // ←何度も繰り返すけど、ここのセミコロン忘れないでね
int main() {
// 複素数を作る
Complex a( 1.0 , 2.0 ) ;
Complex b( 2.0 , 3.0 ) ;
// 複素数の計算
a.print() ;
a.add( b ) ;
a.print() ;
a.mul( b ) ;
a.print() ;
return 0 ;
}
練習課題
- 上記の直交座標系の複素数のクラスのプログラムを入力し、動作を確認せよ。
- このプログラムに減算や除算の処理を追加せよ。
この練習課題は、次週に予定している「曲座標系の複素数クラス」に変更となった場合のプログラムを加え、第1回のレポート課題となります。
創造工学演習・PHPとDB(予備実験)
インターネットを活用したプログラムを作成する場合、データを保存管理するためのデータベースと、データベースのデータを処理するためのプログラム言語が必要となってくる。今回の予備実験では、そのためにリレーショナルデータベースと、Webの動的なプログラム言語である PHP について説明する。
リレーショナル・データベース
データベースは、データを保存し、矛盾が発生しない様に管理してくれるシステムであり、インターネットで活用されている。
データを確実に保存し、矛盾なく扱うためには、本来複雑なプログラムが必要となる。この中で、データを表形式のテーブルを組み合わせて管理するシステムはリレーショナルデータベースと呼ばれる。リレーショナルデータベースでは、データの問い合わせなどの処理が簡単にできるように、SQL と呼ばれる言語を使って処理を行う。
大量のデータをインターネットの中で利用するためには、ネットワークを経由してデータの問い合わせが求められ、有名なデータベースシステムには、Oracle, MySQL などがある。今回の実験では、ネットワーク機能は持たないが簡単な手続きで使うことができる SQLite を使って説明する。
また、今回の予備実験では時間も限られることから、複数の表を組み合わせた SQL の処理については割愛する。
SQLの基本
リレーショナルデータベースでは、データの基本は表形式データであり、1つの表に相当するデータはテーブルと呼ぶ。
以下の様な名前・住所・年齢のデータがあったとすると、1人前のデータをレコードと呼び、name, addr, age といった属性はカラムと呼ぶ。
| name | addr | age | |
| t-saitoh | 越前市 | 55 | ←レコード |
| sakamoto | 福井市 | 50 | |
| murata | 福井市 | 35 | |
| ↑カラム |
データの型には、文字列型(char型,varchar型,text型)や、数値型(integer型,decimal型,real型)などがあり、create table 文にてカラムの型を定義する。
create table テーブルを作る
データベースの表を使う最初には、create table 文を実行する。C言語での struct 文をイメージすると解り易いかもしれないが、データはデータベースの中に永続的に保存されるので、システムを動かす最初に一度実行するだけで良い。
上記のような名前・住所・年齢のデータ構造であれば、次の様な create table 文を使う。
create table テーブル名 (
カラム名1 型1 ,
カラム名2 型2
) ;
-- 例 --
create table PERSON ( -- テーブル名:PERSON
name varchar( 20 ) , -- 名前
addr varchar( 20 ) , -- 住所
age integer , -- 年齢
primary key( name ) -- name はデータ検索のキーであり重複は許されない
) ;
これと同じ様な処理をC言語で書くのであれば、以下の様な構造体宣言と同じであろう。
struct PERSON {
char name[ 20 ] ; // 名前
char addr[ 20 ] ; // 住所
int age ; // 年齢
} ;
drop table テーブルを消す
データベースは永続的に保存されるので、テーブル全体のデータが不要であれば、drop table 命令で、テーブル全体を消す。
drop table テーブル名 ; -- 例 -- drop table PERSON ;
insert into レコードを追加
データベースに1レコードを保存するには、insert文を用いる。
insert into テーブル名 ( カラム名... ) values( 値... ) ;
-- 例 --
insert into PERSON ( name , addr , age )
values ( 't-saitoh' , '越前市' , 55 ) ;
insert into PERSON ( name , addr , age )
values ( 'sakamoto' , '福井市' , 50 ) ;
insert into PERSON ( name , addr , age )
values ( 'murata' , '福井市' , 35 ) ;
delete レコードを消す
データベースのレコードを消すには、delete 文を用いる。条件を満たす複数のデータをまとめて消すことができる。
delete from テーブル名 where 条件 ;
-- 例 --
-- 40歳未満のデータを全て消す。 murata,福井市,35 が消える。
delete from PERSON
where age < 40 ;
update レコードを更新
データベースのレコードを修正するには、update 文を用いる。条件を満たす複数のデータをまとめて修正することもできる。
update テーブル名 set カラム = 値 where 条件 ;
-- 例 --
-- 住所が越前市のレコードの年齢を 0 にする。
update PERSON set age = 0
where addr == '越前市' ;
select データを探す
データベースの内容を参照するための命令が select 文。where を記載することで、特定の条件のデータだけを選択したり、特定のカラムだけを抽出することができる。
select カラム名 from テーブル名 where 条件 ;
-- 例 --
-- PERSON の全データを出力
select * from PERSON ;
-- PERSON の住所が福井市だけを選別し、名前と住所を抽出
select name,addr from PERSON
where addr = '福井市' ;
-- PERSON の年齢の最高値を出力 (集約関数)
select max(age) from PERSON
where addr = '福井市' ;
-- PERSON の年齢条件を満たす人数を数える (集約関数)
select count(name) from PERSON
where age >= 50 ;
動的なプログラム言語とPHP
本来、Webサーバが作られた頃は、論文や研究用のデータを公開する物であったが、扱うデータが増えるにつれ、特定の論文や研究データの一覧を表示したり探したりという処理が求められた。こういった処理のためにWebページのアクセスを受けた時に処理を実行する CGI という機能があったが、これを発展させてできたプログラム言語が PHP である。
PHPでは、ページを表示するための HTML の中に <?php … ?> のといった開始タグ・終了タグの中に、ブラウザから送られてきたデータに合わせて、処理を行うPHPの命令を記述し、データを(一般的にはHTML形式で)表示することができる。基本文法は C 言語に似ているが、様々なデータを扱うために変数にはどのような型でも保存できるようになっている。
ブラウザからデータを送るためのform文
ブラウザで入力欄を作ったり選択肢を表示し、その結果を送るための HTML は、入力フォーム(form)と呼ぶ。
<form method="get" action="処理ページ" >
<input type="text" name="変数名" />
<input type="radio" name="変数名" value="値" />
<input type="checkbox" name="変数名" value="値" />
<textarea cols="横文字数" rows="行数"></textarea>
<select name="変数名">
<option value="値1">表示1</option>
<option value="値2">表示2</option>
</select>
<input type="submit" value="実行ボタンに表示する内容" />
</form>
formでは、入力する項目に変数名の名前を付け、action=”” で示したページにデータを送る。
PHPのプログラムの基本
PHPのプログラムは、外見は一般的に HTML ファイルであり、途中で <?php のタグからは、?> までの範囲が、PHP で処理が行われる。PHP のプログラムで print が実行されると、その場所に print 内容が書かれているような HTML ファイルが生成され、ブラウザで表示される。
PHP の中で変数は、$ で始まり、型宣言は基本的に不要である。
文字データを連結する場合は、“.” 演算子を使う。ダブルクオテーション”…”で囲まれた文字列の中の $名前 の部分は、変数名として扱われ、変数名の内容に置き換えられる。
HTMLのform文の action 属性で示された php であれば、PHPの中で送られてきた値を $_GET[‘変数名’] (method=”get”の場合)、 $_POST[‘変数名’] (method=”post”の場合)、または $_REQUEST[‘変数名’] (method=”get” or “post”) で参照できる。
((( sample.php )))
<html>
<head>
<title>sample.php</title>
<meta http-equiv="Content-Type" content="text/html; charset=utf-8" />
</head>
<body>
<form action="sample.php" method="POST">
<input name="A" type="text" /> <!-- 変数 $A -->
+
<input name="B" type="text" /> <!-- 変数 $B -->
=
<?php
ini_set( 'error_reporting' , E_WARNING ) ;
if ( $_REQUEST[ "A" ] != "" && $_REQUEST[ "B" ] != "" ) {
print $_REQUEST[ "A" ] + $_REQUEST[ "B" ] ;
} else {
print "<INPUT TYPE=submit>" ;
}
?>
</form>
</body>
</html>
PHPでデータベースを扱う
SQLのデータベースを、プログラム言語の中で扱う場合は、その記述も色々である。PHPでは以下の様にSQLを扱う。
((( survey-init.php )))
<html>
<head>
<title>survey_init.php</title>
<meta http-equiv="Content-Type" content="text/html; charset=utf-8" />
</head>
<body>
<?php
// デバッグ用にエラー警告を表示する
ini_set( 'error_reporting' , E_WARNING ) ;
// データベースに接続する
$data_dir = "../public_data" ;
$dbh = new PDO( "sqlite:$data_dir/sqlite.db" ) ;
// データベースを初期化する
$init_sql = "drop table if exists Survey ;"
. "create table Survey ("
. " uid varchar( 20 ) ,"
. " item varchar( 10 )"
. ") ;"
. "insert into Survey ( uid , item ) values ( 't-saitoh' , '猫' ) ;"
. "insert into Survey ( uid , item ) values ( 'tomoko' , 'ケーキ' ) ;"
. "insert into Survey ( uid , item ) values ( 'mitsuki' , 'ボードゲーム' ) ;"
;
if ( $dbh->exec( $init_sql ) < 0 ) {
print "Error: $init_sql" ;
}
// データベースの表形式を読み出し、表形式で出力する。
print "<table border='1'>\n" ;
print "<tr><td align='center'>uid</td><td align='center'>item</td></tr>\n" ;
$select_sql = "select uid,item from Survey ;" ;
foreach( $dbh->query( $select_sql ) as list( $uid , $item ) ) {
print "<tr><td>$uid</td><td>$item</td></tr>\n" ;
}
print "<table>\n" ;
// データベースの単一データを取り出す
$count_sql = "select count(item) from Survey where item = 'ケーキ' ;" ;
print $dbh->query( $count_sql )->fetchColumn() ;
?>
</body>
</html>
PHPの主要なSQL関数(PDO)
$dbh = new PDO(…) ; データベースに接続するハンドラを取得。 $dbh->exec( “create…” ) ; データベースでSQLを実行。 $dbh->query( “select…” ) ; データベースに問い合わせ。「1レコードに対応した配列」が全データだけ繰り返す、2次元配列を返す。 $dbh->query( “…” )->fetchColumn() 結果が1つだけの問い合わせ。集約関数の結果を参照する場合に用いる。
練習問題(1)
- 上記の survey-init.php の select 文の部分を編集し、色々なデータ検索を試してみよ。
入力フォームのデータをデータベースに書き込む
((( survey-vote.php )))
<?php
// エラー警告を表示
ini_set( 'error_reporting' , E_WARNING ) ;
// form から送られてきた変数を保存
$uid = $_REQUEST[ "uid" ] ;
$item = $_REQUEST[ "item" ] ;
// データベースに接続する
$data_dir = "../public_data" ;
$dbh = new PDO( "sqlite:$data_dir/sqlite.db" ) ;
// データベースに項目を追加する
if ( $uid != "" && $item != "" ) {
$insert_sql = sprintf( "insert into Survey( uid , item ) values ( %s , %s ) ;" ,
$dbh->quote( $uid ) , $dbh->quote( $item ) ) ;
$dbh->exec( $insert_sql ) ;
// reload処理で追記しないためページを強制的に再表示させる
header( "Location: survey-vote.php" ) ;
}
?>
<html>
<head>
<title>survey_vote.php</title>
<meta http-equiv="Content-Type" content="text/html; charset=utf-8" />
</head>
<body>
<form method="get" action="survey-vote.php">
名前: <input type="text" name="uid" />
好きな物:<input type="text" name="item" />
<input type="submit" value="投票" />
</form>
<?php
// データベースの表形式を読み出し、表形式で出力する。
print "<table border='1'>\n" ;
print " <tr><td align='center'>uid</td><td align='center'>item</td></tr>\n" ;
$select_sql = "select uid,item from Survey ;" ;
foreach( $dbh->query( $select_sql ) as list( $t_uid , $t_item ) ) {
print " <tr><td>$t_uid</td><td>$t_item</td></tr>\n" ;
}
print "</table>\n" ;
?>
</body>
</html>
練習問題(2)
- 上記の survey-vote.php のプログラムを編集し色々な入力方法・出力方法を試してみよ。
- 例えば、入力の item 選択に select や ラジオボタン フォームを使う。
- 例えば、出力結果で、item の投票結果を、棒グラフで出力する。
JavaScriptによるフロントエンドとPHPバックエンド入門
前回の講義では、インターネットの仕組みを復習し、そこで使われるプログラミング言語などを紹介した。
今回の授業では、インターネットのブラウザ側(フロントエンド)で使われるプログラム言語である JavaScript の基本について整理しなおし、簡単な穴埋め問題による演習を行う。
JavaScriptによるフロントエンドプログラミング
-
- 以下のサンプル(sample3.html~sampleA.html)は、各HTMLファイルを開くとソースコードが表示されます。JavaScriptによるプログラムなので、自分のパソコンにダウンロードし、演習についてはダウンロードしたファイルを編集して、ブラウザで動作を確認してください。
- sample3.html
- sample4.html
- sample5.html
- sample6.html — 簡単な穴埋め問題
- sample7.html
- sample8.html
- sample9.html — 簡単な穴埋め問題
- sampleA.html
- sampleA.css
- 以下のサンプル(sampleB2.html~sampleC2.html)は、jquery が html ファイルと同じ場所に置いてある必要があり、ダウンロードしたファイルを開いてもこのままでは動きません。動作確認のページにて実行結果を確認してください。
- sampleB2.html 動作確認Webページ
- sampleC2.html 動作確認Webページ
- sampleC.json
- 無名関数の説明
- 練習問題 6 , 9 の提出先
- 2024/情報メディア工学(4/24)小テスト
再帰呼び出しと処理時間の見積もり
前回の講義で説明できなかった、オーダーの問題の解説
練習問題
の処理時間を要するアルゴリズム(データ件数が変わっても処理時間は一定)を、オーダー記法で書くとどうなるか?また、このような処理時間となるアルゴリズムの例を答えよ。
- ある処理のデータ数Nに対する処理時間が、
であった場合、オーダー記法で書くとどうなるか?
の処理時間を要するアルゴリズムを、オーダー記法で書くとどうなるか?
(ヒント: ロピタルの定理)
- 1は、O(1)。
- 誤答の例:O(0)と書いちゃうと、T(N)=Tα×0=0になってしまう。
- 事例は、電話番号を、巨大配列の”電話番号”番目の場所に記憶するといった方法。(これはハッシュ法で改めて講義予定)
- 2は、N→∞において、N2 ≪ 2Nなので、O(2N) 。厳密に回答するなら、練習問題3と同様の証明が必要。
- 3の解説
再帰呼び出しの基本
次に、再帰呼び出しを含むような処理の処理時間見積もりについて解説をおこなう。そのまえに、再帰呼出しと簡単な処理の例を説明する。
再帰関数は、自分自身の処理の中に「問題を小さくした」自分自身の呼び出しを含む関数。プログラムには問題が最小となった時の処理があることで、再帰の繰り返しが止まる。
// 階乗 (末尾再帰)
int fact( int x ) {
if ( x <= 1 )
return 1 ;
else
return x * fact( x-1 ) ;
}
// ピラミッド体積 (末尾再帰)
int pyra( int x ) {
if ( x <= 1 )
return 1 ;
else
return x*x + pyra( x-1 ) ;
}
// フィボナッチ数列 (非末尾再帰)
int fib( int x ) {
if ( x <= 2 )
return 1 ;
else
return fib( x-1 ) + fib( x-2 ) ;
}
階乗 fact(N) を求める処理は、以下の様に再帰が進む。(N=5の場合)

また、フィボナッチ数列 fib(N) を求める処理は以下の様に再帰が進む。(N=5の場合)

再帰呼び出しの処理時間
次に、この再帰処理の処理時間を説明する。 最初のfact(),pyra()については、 x=1の時は、関数呼び出し,x<=1,return といった一定の処理時間を要し、T(1)=Ta で表せる。 x>1の時は、関数呼び出し,x<=1,*,x-1,returnの処理(Tb)に加え、x-1の値で再帰を実行する処理時間T(N-1)がかかる。 このことから、 T(N)=Tb=T(N-1)で表せる。
} 再帰方程式
このような、式の定義自体を再帰を使って表した式は再帰方程式(漸化式)と呼ばれる。これを以下のような代入の繰り返しによって解けば、一般式 が得られる。
T(1)=Ta
T(2)=Tb+T(1)=Tb+Ta
T(3)=Tb+T(2)=2×Tb+Ta
:
T(N)=Tb+T(N-1)=Tb + (N-2)×Tb+Ta
一般的に、再帰呼び出しプログラムは(考え方に慣れれば)分かりやすくプログラムが書けるが、プログラムを実行する時には、局所変数や関数の戻り先を覚える必要があり、深い再帰ではメモリ使用量が多くなる。
ただし、fact() や pyra() のような関数は、プログラムの末端で再帰が行われている。(fib()は、再帰の一方が末尾ではない)
このような再帰は、末尾再帰(tail recursion) と呼ばれ、関数呼び出しの return を、再帰処理の先頭への goto 文に書き換えるといった最適化が可能である。言い換えるならば、末尾再帰の処理は繰り返し処理に書き換えが可能である。このため、末尾再帰の処理をループにすれば再帰のメモリ使用量の問題を克服できる。
再帰を含む一般的なプログラム例
ここまでのfact()やpyra()のような処理の再帰方程式は、再帰の度にNの値が1減るものばかりであった。もう少し一般的な再帰呼び出しのプログラムを、再帰方程式で表現し、処理時間を分析してみよう。
以下のプログラムを実行したらどんな値になるであろうか?それを踏まえ、処理時間はどのように表現できるであろうか?
// 分割統治法による配列合計
#include <stdio.h>
int sum( int a[] , int L , int R ) { // 非末尾再帰
// L : 左端のデータ
// R : 右端のデータが入っているの場所+1
if ( R - L == 1 ) {
return a[ L ] ;
} else {
int M = (L + R) / 2 ;
return sum( a , L , M ) + sum( a , M , R ) ;
}
}
int main() {
int array[ 8 ] = {
// L=0 1 2 3 4 5 6 7 R=8
3 , 6 , 9 , 1 , 8 , 2 , 4 , 5 ,
} ;
printf( "%d¥n" , sum( array , 0 , 8 ) ) ;
return 0 ;
}
// 分割統治法による配列合計
import java.util.*;
public class Main {
static int sum( int a[] , int L , int R ) { // 非末尾再帰
// L : 左端のデータ
// R : 右端のデータが入っているの場所+1
if ( R - L == 1 ) {
return a[ L ] ;
} else {
int M = (L + R) / 2 ;
return sum( a , L , M ) + sum( a , M , R ) ;
}
}
public static void main(String[] args) throws Exception {
int array[] = {
// L=0 1 2 3 4 5 6 7 R=8
3 , 6 , 9 , 1 , 8 , 2 , 4 , 5 ,
} ;
System.out.println( sum( array , 0 , array.length ) );
}
}
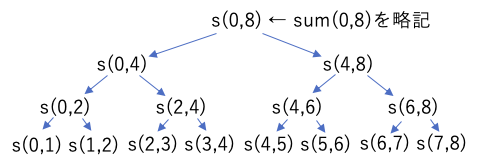
このプログラムでは、配列の合計を計算しているが、引数の L,R は、合計範囲の 左端(左端のデータのある場所)・右端(右端のデータのある場所+1)を表している。そして、再帰のたびに2つに分割して解いている。
このような、処理を(この例では半分に)分割し、分割したそれぞれを再帰で計算し、その処理結果を組み合わせて最終的な結果を求めるような処理方法を、分割統治法と呼ぶ。
このプログラムでは、対象となるデータ件数(R-L)をNとおいた場合、実行される命令からsum()の処理時間Ts(N)は次の再帰方程式で表せる。
← Tβ + (L〜M)の処理時間 + (M〜R)の処理時間
これを代入の繰り返しで解いていくと、
ということで、このプログラムの処理時間は、 で表せる。
ハノイの塔
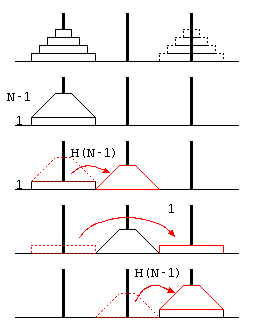 ここまでは、簡単な再帰呼び出しのプログラムを例にして再帰方程式などの説明を行った。次に「ハノイの塔」の処理時間を例題に、プログラムの処理時間について分析を行う。
ここまでは、簡単な再帰呼び出しのプログラムを例にして再帰方程式などの説明を行った。次に「ハノイの塔」の処理時間を例題に、プログラムの処理時間について分析を行う。
ハノイの塔は、3本の塔にN枚のディスクを積み、(1)1回の移動ではディスクを1枚しか動かせない、(2)ディスクの上により大きいディスクを積まない…という条件で、山積みのディスクを目的の山に移動させるパズル。
一般解の予想
ハノイの塔の移動回数を とした場合、 少ない枚数での回数の考察から、 以下の一般式で表せることが予想できる。
… ①
この予想が常に正しいことを証明するために、ハノイの塔の処理を、 最も下のディスク1枚への操作と、その上の(N-1)枚のディスクへの操作に分けて考える。
再帰方程式
上記右の図より、N枚の移動をするためには、上に重なるN-1枚を移動させる必要があるので、
… ②
… ③
ということが言える。(これがハノイの塔の移動回数の再帰方程式)
ディスクが枚の時、予想①が正しいのは明らか①,②。
ディスクが 枚で、予想が正しいと仮定すると、
枚では、
… ③より
… ①を代入
… ①の
の場合
となり、 枚でも、予想が正しいことが証明された。 よって数学的帰納法により、1枚以上で予想が常に成り立つことが証明できた。
また、ハノイの塔の処理時間は、で表せる。
引数の取扱いとオブジェクト指向の導入
値渡し,ポインタ渡し,参照渡し
C言語をあまりやっていない学科の人向けのC言語の基礎として、関数との値渡し, ポインタ渡しについて説明する。ただし、参照渡しについては電子情報の授業でも細かく扱っていない内容なので電子情報系学生も要注意。
オブジェクト指向のプログラムでは、構造体のポインタ渡し(というよりは参照渡し)を多用するが、その基本となる関数との値の受け渡しの理解のため、以下に値渡し・ポインタ渡し・参照渡しについて説明する。
ポインタと引数
値渡し(call by value, pass by value)
// 値渡しのプログラム
void foo( int x ) { // x は局所変数(仮引数は呼出時に
// 対応する実引数で初期化される。
x++ ;
printf( "%d¥n" , x ) ;
}
int main() {
int a = 123 ;
foo( a ) ; // 124
// 処理後も main::a は 123 のまま。
foo( a ) ; // 124
return 0 ;
}
このプログラムでは、aの値は変化せずに、124,124 が表示される。ここで、関数 foo() を呼び出しても、関数に「値」が渡されるだけで、foo() を呼び出す際の実引数 a の値は変化しない。こういった関数に値だけを渡すメカニズムは「値渡し」と呼ぶ。
値渡しだけが使われれば、関数の処理後に変数に影響が残らない。こういった処理の影響が残らないことは一般的に「副作用がない」という。
大域変数を使ったプログラム
でも、プログラムによっては、124,125 と変化して欲しい場合もある。どのように記述すべきだろうか?
// 大域変数を使う場合
int x ;
void foo() {
x++ ;
printf( "%d¥n" , x ) ;
}
int main() {
x = 123 ;
foo() ; // 124
foo() ; // 125
return 0 ;
}
しかし、このプログラムは大域変数を使うために、間違いを引き起こしやすい。大域変数はどこでも使える変数であり、副作用が発生して間違ったプログラムを作る原因になりやすい。
// 大域変数が原因で予想外の挙動をしめす簡単な例
int i ;
void foo() {
for( i = 0 ; i < 2 ; i++ )
printf( "A" ) ;
}
int main() {
for( i = 0 ; i < 3 ; i++ ) // このプログラムでは、AA AA AA と
foo() ; // 表示されない。
return 0 ;
}
ポインタ渡し(call by pointer, pass by pointer)
C言語で引数を通して、呼び出し側の値を変化して欲しい場合は、変更して欲しい変数のアドレスを渡し、関数側では、ポインタ変数を使って受け取った変数のアドレスの示す場所の値を操作する。(副作用の及ぶ範囲を限定する) こういった、値の受け渡し方法は「ポインタ渡し」と呼ぶ。
// ポインタ渡しのプログラム
void foo( int* p ) { // p はポインタ
(*p)++ ;
printf( "%d¥n" , *p ) ;
}
int main() {
int a = 123 ;
foo( &a ) ; // 124
// 処理後 main::a は 124 に増えている。
foo( &a ) ; // 124
return 0 ; // さらに125と増える
}
ポインタを利用して引数に副作用を与える方法は、ポインタを正しく理解していないプログラマーでは、危険な操作となる。
参照渡し(call by reference, pass by reference)
C++では、ポインタ渡しを極力使わないようにするために、参照渡しを利用する。ただし、ポインタ渡しも参照渡しも、機械語レベルでは同じ処理にすぎない。
// ポインタ渡しのプログラム void foo( int& x ) { // xは参照 x++ ; printf( "%d¥n" , x ) ; } int main() { int a = 123 ; foo( a ) ; // 124 // 処理後 main::a は 124 に増えている。 foo( a ) ; // 124 return 0 ; // さらに125と増える。 }
大きなプログラムを作る場合、副作用のあるプログラムの書き方は、間違ったプログラムの原因となりやすい。そこで関数の呼び出しを中心としてプログラムを書くものとして、関数型プログラミングがある。
構造体の参照渡し
構造体のデータを関数で受け渡しをする場合は、参照渡しを利用する。
struct Person {
char name[ 20 ] ;
int age ;
} ;
void print( struct Person* p ) {
printf( "%s %d¥n" , p->name , p->age ) ;
}
void main() {
struct Person saitoh ;
strcpy( saitoh.name , "t-saitoh" ) ;
saitoh.age = 50 ;
print( &saitoh ) ; // ポインタによる参照渡し
}
このようなプログラムの書き方をすると、「データ saitoh に、print() せよ…」 といった処理を記述したようになる。 これを発展して、データ saitoh に、print という命令をするイメージにも見える。
この考え方を、そのままプログラムに反映させ、Personというデータは、 名前と年齢、データを表示するprintは…といったように、 データ構造と、そのデータ構造への処理をペアで記述すると分かりやすい。
オブジェクト指向の導入
構造体でオブジェクト指向もどき
例えば、名前と年齢の構造体で処理を記述する場合、 以下の様な記載を行うことで、データ設計者とデータ利用者で分けて 仕事ができることを説明。
// この部分はデータ構造の設計者が書く
// データ構造を記述
struct Person {
char name[10] ;
int age ;
} ;
// データに対する処理を記述
void setPerson( struct Person* p , char s[] , int a ) {
// ポインタの参照で表記
strcpy( (*p).name , s ) ;
(*p).age = a ;
}
void printPerson( struct Person* p ) {
// アロー演算子で表記 "(*p).name" は "p->name" で書ける
printf( "%s %d¥n" ,
p->name , p->age ) ;
}
// この部分は、データ利用者が書く
int main() {
// Personの中身を知らなくてもいいから配列を定義(データ隠蔽)
struct Person saitoh ;
setPerson( &saitoh , "saitoh" , 55 ) ;
struct Person table[ 10 ] ; // 初期化は記述を省略
for( int i = 0 ; i < 10 ; i++ ) {
// 出力する...という雰囲気で書ける(手続き隠蔽)
printPerson( &table[i] ) ;
}
return 0 ;
}
このプログラムの書き方では、mainの中を読むだけもで、 データ初期化とデータ出力を行うことはある程度理解できる。 この時、データ構造の中身を知らなくてもプログラムが理解でき、 データ実装者はプログラムを記述できる。これをデータ構造の隠蔽化という。 一方、setPerson()や、printPerson()という関数の中身についても、 初期化・出力の方法をどうするのか知らなくても、 関数名から動作は推測できプログラムも書ける。 これを手続きの隠蔽化という。
C++のクラスで表現
上記のプログラムをそのままC++に書き直すと以下のようになる。
#include <stdio.h>
#include <string.h>
// この部分はクラス設計者が書く
class Person {
private: // クラス外からアクセスできない部分
// データ構造を記述
char name[10] ; // メンバーの宣言
int age ;
public: // クラス外から使える部分
// データに対する処理を記述
void set( char s[] , int a ) { // メソッドの宣言
// pのように対象のオブジェクトを明記する必要はない。
strcpy( name , s ) ;
age = a ;
}
void print() {
printf( "%s %d¥n" , name , age ) ;
}
} ; // ← 注意ここのセミコロンを書き忘れないこと。
// この部分はクラス利用者が書く
int main() {
Person saitoh ;
saitoh.set( "saitoh" , 55 ) ;
saitoh.print() ;
// 文法エラーの例
printf( "%d¥n" , saitoh.age ) ; // age は private なので参照できない。
return 0 ;
}
用語の解説:C++のプログラムでは、データ構造とデータの処理を、並行しながら記述する。 データ構造に対する処理は、メソッド(method)と呼ばれる。 データ構造とメソッドを同時に記載したものは、クラス(class)と呼ぶ。 そのclassに対し、具体的な値や記憶域が割り当てられたものをオブジェクト(object)と呼ぶ。
Webページの生成とプログラム言語
前回の講義では、OSの仕組みとインターネット(Web)の仕組みについて、総括・復習をおこなった。
2回目の授業では、インターネットのWebページを作るために使われているHTMLやCSSやプログラム言語について解説を行う。
Webページの生成とプログラム言語
理解確認
- こちらの小テストに回答してください。
繰り返し処理と処理時間の見積もり
単純サーチの処理時間
ここで、プログラムの実行時間を細かく分析してみる。
// ((case-1))
// 単純サーチ O(N)
#include <stdio.h>
int main() {
int a[ 10 ] = {
12 , 64 , 35 , 29 , 59 , 9 , 83 , 73 , 21 , 61
} ;
int N = 10 ; // 実際のデータ数(Nとする)
int key = 21 ; // 探すデータ
for( int i = 0 ; i < N ; i++ )
if ( a[i] == key )
break ;
return 0 ;
}
import java.util.*;
public class Main {
public static void main(String[] args) throws Exception {
// Your code here!
int a[] = {
12 , 64 , 35 , 29 , 59 , 9 , 83 , 73 , 21 , 61
} ;
int N = a.length ;
int key = 21 ;
for( int i = 0 ; i < N ; i++ )
if( a[i] == key )
break ;
}
}
例えばこの 単純サーチをフローチャートで表せば、以下のように表せるだろう。フローチャートの各部の実行回数は、途中で見つかる場合があるので、最小の場合・最大の場合を考え平均をとってみる。また、その1つ1つの処理は、コンピュータで機械語で動くわけだから、処理時間を要する。この時間を ,
,
,
とする。
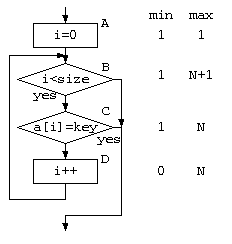
この検索処理全体の時間 を考えると、平均時間とすれば、以下のように表せるだろう。
ここで例題
この単純サーチのプログラムを動かしてみたら、N=1000で、5μ秒かかったとする。では、N=10000であれば、何秒かかるだろうか?
感のいい学生であれば、直感的に 50μ秒 と答えるだろうが、では、Tβ,Tα は何秒だったのだろうか? 上記のT(N)=Tα+N ✕ Tβ に当てはめると、N=1000,T(N)=5μ秒の条件では、連立方程式は解けない。
ここで一番のポイントは、データ処理では N が小さな値の場合(データ件数が少ない状態)はあまり考えない。N が巨大な値であれば、Tαは、1000Tβに比べれば微々たる値という点である。よって
で考えれば良い。これであれば、T(1000)=5μ秒=Tβ×1000 よって、Tβ=5n秒となる。この結果、T(10000)=Tβ×10000=50μ秒 となる。
2分探索法と処理時間
次に、単純サーチよりは、速く・プログラムとしては難しくなった方法として、2分探索法の処理時間を考える。データはあらかじめ昇順に並べておくことで、一度の比較で対象件数を減らすことで高速に探すことができる。
下記プログラムを読む場合の注意点:
- Lは、探索範囲の一番左端のデータのある場所。
- Rは、探索範囲の一番右端のデータのある場所 + 1
// ((case-2))
// 2分探索法 O(log N)
#include <stdio.h>
int main() {
int a[] = {
9 , 12 , 21 , 29 , 35 , 59 , 61 , 64 , 73 , 83
} ;
int L = 0 ; // L : 左端のデータの場所
int R = 10 ; // R : 右端のデータの場所+1
while( L != R ) {
int M = (L + R) / 2 ;
if ( a[M] == key )
break ;
else if ( a[M] < key )
L = M + 1 ;
else
R = M ;
}
return 0 ;
}
import java.util.*;
public class Main {
public static void main(String[] args) throws Exception {
int a[] = {
9 , 12 , 21 , 29 , 35 , 59 , 61 , 64 , 73 , 83
} ;
int L = 0 ; // L : 左端のデータの場所
int R = a.length ; // R : 右端のデータの場所+1
int key = 73 ;
while( L != R ) {
int M = (L + R) / 2 ;
if ( a[M] == key )
break ;
else if ( a[M] < key )
L = M + 1 ;
else
R = M ;
}
}
}
このプログラムでは、1回のループ毎に対象となるデータ件数は、となる。説明を簡単にするために1回毎にN/2件となると考えれば、M回ループ後は、
件となる。データ件数が1件になれば、データは必ず見つかることから、以下の式が成り立つ。
…両辺のlogをとる
2分探索は、繰り返し処理であるから、処理時間は、
… (Mはループ回数)
ここで、本来なら log の底は2であるが、後の見積もりの例では、問題に応じて底変換の公式 ()で係数が出てくるが、これはTβに含めて考えればいい。
単純なソート(選択法)の処理時間
次に、並べ替え処理の処理時間について考える。
単純な並べ替えアルゴリズムとしてはバブルソートなどもあるが、2重ループの内側のループ回数がデータによって変わるので、選択法で考える。
// ((case-3))
// 選択法 O(N^2)
#include <stdio.h>
int main() {
int a[] = {
12 , 64 , 35 , 29 , 59 , 9 , 83 , 73 , 21 , 61
} ;
int size = 10 ;
for( int i = 0 ; i < size - 1 ; i++ ) {
int tmp ;
// i..size-1 の範囲で一番大きいデータの場所を探す
int m = i ;
for( int j = i + 1 ; j < size ; j++ ) {
if ( a[j] > a[m] )
m = j ;
}
// 一番大きいデータを先頭に移動
tmp = a[i] ;
a[i] = a[m] ;
a[m] = tmp ;
}
return 0 ;
}
import java.util.*;
public class Main {
public static void main(String[] args) throws Exception {
int a[] = {
12 , 64 , 35 , 29 , 59 , 9 , 83 , 73 , 21 , 61
} ;
int size = a.length ;
for( int i = 0 ; i < size - 1 ; i++ ) {
int tmp ;
int m = i ;
for( int j = i + 1 ; j < size ; j++ ) {
if ( a[j] > a[m] )
m = j ;
}
tmp = a[i] ;
a[i] = a[m] ;
a[m] = tmp ;
}
}
}
このプログラムの処理時間T(N)は…
… i=0の時
… i=1の時
:
… i=N-1の時
…(参考 数列の和の公式)
となる。
オーダー記法
ここまでのアルゴリズムをまとめると以下の表のようになる。ここで処理時間に大きく影響する部分は、最後の項の部分であり、特にその項の係数は、コンピュータの処理性能に影響を受けるが、アルゴリズムの優劣を考える場合は、それぞれ、
の部分の方が重要である。
| 単純サーチ | |
| 2分探索法 | |
| 最大選択法 |
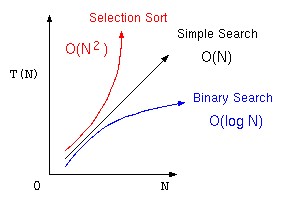
そこで、アルゴリズムの優劣を議論する場合は、この処理時間の見積もりに最も影響する項で、コンピュータの性能によって決まる係数を除いた部分を抽出した式で表現する。これをオーダー記法と言う。
| 単純サーチ | オーダーNのアルゴリズム | |
| 2分探索法 | オーダー log N のアルゴリズム | |
| 最大選択法 | オーダー N2 のアルゴリズム |
練習問題
- ある処理のデータ数Nに対する処理時間が、
であった場合、オーダー記法で書くとどうなるか?
- コンピュータで2分探索法で、データ100件で10[μsec]かかったとする。
データ10000件なら何[sec]かかるか?
(ヒント: 底変換の公式) の処理時間を要するアルゴリズム(データ件数が変わっても処理時間は一定)を、オーダー記法で書くとどうなるか?また、このような処理時間となるアルゴリズムの例を答えよ。
の処理時間を要するアルゴリズムを、オーダー記法で書くとどうなるか?
(ヒント: ロピタルの定理)
- 2と4の解説
- 1は、N→∞において、N2 ≪ 2Nなので、O(2N) 。厳密に回答するなら、練習問題4と同様の証明が必要。
- 3は、O(1)。
- 誤答の例:O(0)と書いちゃうと、T(N)=Tα×0=0になってしまう。
- 事例は、電話番号を、巨大配列の”電話番号”番目の場所に記憶するといった方法。(これはハッシュ法で改めて講義予定)

