ホーム » 2022
年別アーカイブ: 2022
緊急連絡システムサーバ移転
Azureサーバ上で動かしていた緊急連絡システムだけど、azure 仮想マシン(クラッシック) で構築してあったけど、クラッシックが2023/3月より動かなくなるので 最近の仮想マシン形式(ARM)のサーバに移転。
といっても、またサーバ移転しなくちゃいけなくなりそうだけど。
qmailからpostfixに移行
これに合わせて以前より問題となっていた qmail ベースで一部サーバにメールが届かない(設定触って届くようにしているけど…)問題を解決。postfix での配送になったので、大量メールでの配送遅延は大きくなったかもしれないけど、さほど影響しないはず。
DKIM, SPF 対応
メール配信に postfix を使うようにしたから、メールの認証も SPF だけでなく opendkim を使って DKIM にも対応させてみた。現時点では、DNS 設定の修正が完全に終われば、spam 扱いも改善されるはず。

SPF は、ドメインから発信されるメールサーバ情報を DNS で公開することで、不正なメール発信を防ぐ方式。DKIM は、DNS に登録してある公開鍵と、個別のメールに付けられる公開鍵を比較することで、不正なメール発信を確認できる仕組み。
ハッシュ衝突対策と文字列のハッシュ関数
前回の授業で説明したハッシュ法は、データから簡単な計算(ハッシュ関数)で求まるハッシュ値をデータの記憶場所とする。しかし、異なるデータでも同じハッシュ値が求まった場合、どうすれば良いか?
ハッシュ法を簡単なイメージで説明すると、100個の椅子(ハッシュ表)が用意されていて、1クラスの学生が自分の電話番号の末尾2桁(ハッシュ関数)の場所(ハッシュ値)に座るようなもの。自分のイスに座ろうとしたら、同じハッシュ値の人が先に座っていたら、どこに座るべきだろうか?
オープンアドレス法
先の椅子取りゲームの例え話であれば、先に座っている人がいた場合、最も簡単な椅子に座る方法は、隣が空いているか確認して空いていたらそこに座ればいい。
これをプログラムにしてみると、以下のようになる。このハッシュ法は、求まったアドレスの場所にこだわらない方式でオープンアドレス法と呼ばれる。
// オープンアドレス法
// table[] は大域変数で0で初期化されているものとする。
// 配列に電話番号と名前を保存
void entry( int phone , name ) {
int idx = hash_func( phone ) ;
while( table[ idx ].phone != 0 )
idx = (idx + 1) % HASH_SIZE ; // ひとつ後ろの席
} // idx++ でないのは何故?
table[ idx ].phone = phone ;
strcpy( table[ idx ].name , name ) ;
}
// 電話番号から名前を調べる
char* search( int phone ) {
int idx = hash_func( phone ) ;
while( table[ idx ].phone != 0 ) {
if ( table[ idx ].phone == phone )
return table[ idx ].name ;
idx = (idx + 1) % HASH_SIZE ; // ひとつ後ろの席
} // idx++ でないのは何故?
return NULL ; // 見つからなかった
}
注意:このプログラムは、ハッシュ表すべてにデータが埋まった場合、無限ループとなるので、実際にはもう少し改良が必要である。
この実装方法であれば、ハッシュ表にデータが少ない場合は、ハッシュ値を計算すれば終わり。よって、処理時間のオーダはO(1)となる。しかし、ハッシュ表がほぼ埋まっている状態だと、残りわずかな空き場所を探すようなもの。
チェイン法
前に述べたオープンアドレス法は、ハッシュ衝突が発生した場合、別のハッシュ値を求めそこに格納する。配列で実装した場合であれば、ハッシュ表のサイズ以上の データ件数を保存することはできない。
チェイン法は、同じハッシュ値のデータをグループ化して保存する方法。 同じハッシュ値のデータは、リスト構造とするのが一般的。ハッシュ値を求めたら、そのリスト構造の中からひとつづつ目的のデータを探す処理となる。
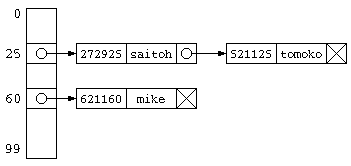
この処理にかかる時間は、データ件数が少なければ、O(1) となる。しかし、ハッシュ表のサイズよりかなり多いデータ件数が保存されているのであれば、ハッシュ表の先に平均「N/ハッシュ表サイズ」件のデータがリスト構造で並んでいることになるので、O(N) となってしまう。
#define SIZE 100
int hash_func( int ph ) {
return ph % SIZE ;
}
struct PhoneNameList {
int phone ;
char name[ 20 ] ;
struct PhoneNameList* next ;
} ;
struct PhoneNameList* hash[ SIZE ] ; // NULLで初期化
struct PhoneNameList* cons( int ph ,
char* nm ,
struct PhoneNameList* nx ) {
struct PhoneNameList* ans ;
ans = (struct PhoneNameList*)malloc(
sizeof( struct PhoneNameList ) ) ;
if ( ans != NULL ) {
ans->phone = ph ;
strcpy( ans->name , nm ) ;
ans->next = nx ;
}
return ans ;
}
void entry( int phone , char* name ) {
int idx = hash_func( phone ) ;
hash[ idx ] = cons( phone , name , hash[ idx ] ) ;
}
char* search( int phone ) {
int idx = hash_func( phone ) ;
struct PhoneNameList* p ;
for( p = hash[ idx ] ; p != NULL ; p = p->next ) {
if ( p->phone == phone )
return p->name ;
}
return NULL ;
}
文字列のハッシュ値
ここまでで説明した事例は、電話番号をキーとするものであり、余りを求めるだけといったような簡単な計算で、ハッシュ値が求められた。しかし、一般的には文字列といったような名前から、ハッシュ値が欲しいことが普通だろう。
ハッシュ値は、簡単な計算で、見た目デタラメな値が求まればいい。 (ただしく言えば、ハッシュ値の出現確率が極力一様であること)。一見規則性が解らない値として、文字であれば文字コードが考えられる。複数の文字で、これらの文字コードを加えるなどの計算をすれば、 偏りの少ない値を取り出すことができる。
int hash_func( char s[] ) {
int sum = 0 ;
for( int i = 0 ; s[i] != '¥0' ; i++ ) {
sum = sum + s[i] ;
}
return sum % SIZE ;
}
文字列順で異なる値となるように
前述のハッシュ関数は、”ABC”さんと”CBA”さんでは、同じハッシュ値が求まってしまう。文字列順で異なる値が求まるように改良してみる。
int hash_func( char s[] ) {
int sum = 0 ;
for( int i = 0 ; s[i] != '¥0' ; i++ ) {
sum = sum*2 + s[i] ;
// sum = (sum * 小さい素数 + s[i]) % 大きい素数 ;
}
return sum % SIZE ;
}
上記のプログラムの、sum = sum*2 + s[i] では、2倍していった数を最後に SIZE で割っているだけなので、文字が長い場合文字コードの値の違いが sum の中に残らない場合も考えられる。こういった場合には、以下のような方法も考えられる。大きな素数で割ることで、余りの中に、元の数の値の違いの影響が残る。これは、疑似乱数生成での剰余法(or 線形合同法)の考え方を取り入れた方法ともいえる。
#define PRIME_B 大きな素数
#define PRIME_A 小さな素数
int hash_func( char s[] ) {
int sum = 0 ;
for( int i = 0 ; s[i] != '¥0' ; i++ ) {
sum = (sum * PRIME_A + s[i]) % PRIME_B ;
}
return sum % SIZE ;
}
ポート番号とメールが届くまで
ポート番号
サーバとなるコンピュータでは、1台のコンピュータで様々なサービスを提供することから、サービスを区別する必要がある。このためにポート番号が使われる。1台毎のコンピュータに割り当てられたIPアドレスを電話番号に例えるなら、ポート番号は内線電話番号に例えることができる。
サーバと通信する場合、サービスを提供するプログラムに応じて標準的なポート番号が決められている。サーバに届いたパケットは、ポート番号に応じてサービスプログラムを起動する。以下の表によく使われるポート番号の一例をあげる。
| ポート番号 | プロトコル | 概要 |
| 20 | ftp | ファイル転送(データ) |
| 21 | ftp | ファイル転送(命令) |
| 22 | ssh | リモート接続(暗号対策あり) |
| 23 | telnet | リモート接続(暗号化なし) |
| 25 | smtp | 電子メール送信 |
| 465 | smtps | 電子メール送信(暗号化) |
| 53 | DNS | ドメインネームサービス |
| 80 | http | Web |
| 443 | https | Web(暗号化) |
| 110 | pop3 | メールダウンロード |
| 995 | pop3s | メールダウンロード(暗号化) |
| 143 | imap | メール閲覧 |
| 993 | imaps | メール閲覧(暗号化) |
| 137,138,139 | netbios | Windows のファイル共有 |
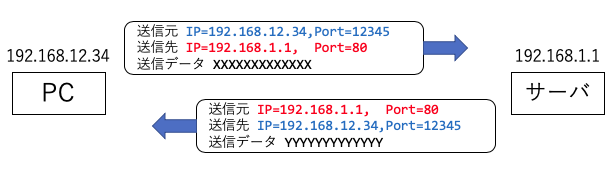
通信パケットには、送信元IPアドレス、送信元ポート番号、送信先IPアドレス、送信先ポート番号の情報がある。
パソコンがサーバと通信する場合は、(1)自分のIPアドレスを送信元IPアドレス、(2)その時に使われていないポート番号をランダムに選び、送信元ポート番号とする。(3)通信相手のIPアドレスと、(4)通信先のサービスのポート番号をセットして、パケットを送付する。サーバは、サービスを要求してきたクライアントの送信先ポート番号をみて、対応するサーバのプログラムを起動する。プログラムの結果を送り返す時は、送信元と送信先のIPアドレス、ポート番号を入替えてパケットを送信する。
1024未満のポート番号(ウェルノウンポート番号)は、サービスを受けとるために用途が決められているので、通常の通信プログラムでは使われない。これ以外のポート番号は、通信の送信元のポート番号として使われ、エフェメラルポート番号と呼ばれる。
ファイアウォール
ネットワークのサービスの中には、組織外に見せたくないものも多い。また、インターネットでは、悪意のあるプログラマが通信して攻撃を加えてくるかもしれない。こういった場合には、ルータなどで、パケットの送信相手のポート番号や、送信元のIPアドレスをみて、パケットを廃棄する場合がある。こういう、ネットワークからの攻撃を防ぐ装置は、ファイアウォール(防火壁)と呼ばれる。
メールが届くまで
電子メールは、非常に迅速にメッセージを相手に届けることができ、そのメッセージを蓄積・加工・編集・転送できる。また、音声や画像といった情報も、複雑な文字情報に置き換えることで、転送できるようになっている。
メールは、利用者のコンピュータに直接届けられるわけではなく、多くの場合はメールを蓄積するメールサーバに送られる。利用者がメールを読む場合、メールサーバから自分の端末に蓄積されたメッセージを読み込み、メッセージを確認する。このメールのやり取りにおいて、メールを送る時、あるいはメールサーバ間でメールを中継するときには、SMTP(Simple Mail Transfer Protocol) が用いられる。一方、メールサーバからメール
を読み出すときには、POP(Post Office Protocol) やIMAP(Internet Message Access Protocol) と呼ばれるプロトコルが用いられる。最近では、IMAPを使ったメールの読み書きをブラウザの中で実行できる WebMail が使われることが増えている。
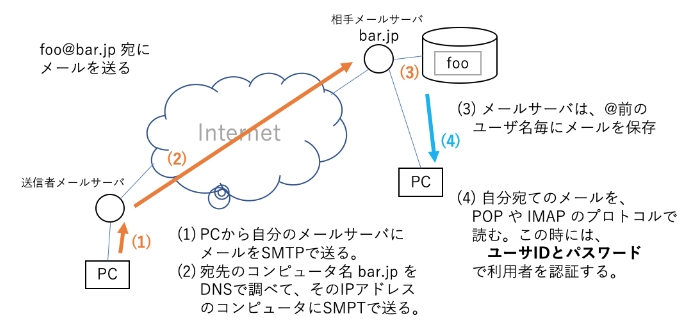
メールが届くまでの流れは、aさんが”foo@bar.jp”に送る場合、
- aさんは、自分の組織のメールサーバに、SMTPでメールを送る。
- メールサーバは、メールアドレスのコンピュータ名部分”bar.jp”をDNSに問合せ、そのIPアドレスを調べ、そのコンピュータにSMTPでメールを送る。
- “bar.jp”のメールサーバは、メールアドレスのユーザ名部分を取り出し、各ユーザ毎にメールを保存する。
- “foo”さんは、自分宛のメールを確認するために、POPまたはIMAPで自分のメールサーバ”bar.jp”に接続し、ユーザ名,パスワードで認証して自分宛のメールを受け取る。
上記の手順2で、相手のメールサーバに直接送れない場合は、コンピュータ名のMXレコードをDNSに問合せを行い、そこで得られたメールサーバに中継を依頼する。
$ nslookup -query=MX fukui-nct.ac.jp. Non-authoritative answer: fukui-nct.ac.jp mail exchanger = 10 fukuinct-ac-jp01c.mail.protection.outlook.com.
POPは、一般的に、メールサーバから自分のメールをダウンロードして削除してしまうため、メールはダウンロードしたコンピュータにしか残らない。このため、様々なコンピュータでメールを読む人には不便となってきた。IMAPでは、メールを読んでも、サーバに残しておく方式であり、別のコンピュータを使う時にもサーバに残っているメールを読むことができる。
通常、SMTPでメールを送る際には、ユーザ認証が行われない。このため、ウィルスに感染したプログラムから迷惑メールを出すことに利用されることが多い。そこで、SMTP送信の前にPOP/IMAP接続しユーザ認証を行った時だけメールを送れる、POP before SMTP(or IMAP before SMTP)といった方式をとる場合もある。
理解度確認
- メールの送信から受信までの処理を、それに使われるプロトコルを交えて説明せよ。
ドメイン名とDNS
ドメイン名とDNS
インターネットでの通信では、IPプロトコルでコンピュータを指定するが、IPアドレスは無機質で覚えるのが大変であり、コンピュータに名前をつけて利用する。この際に、コンピュータの所属などが分かるようにしたものをドメイン名と呼ぶ。
例えば、電子情報工学科のドメイン名 www.ei.fukui-nct.ac.jp は、ピリオド部分で区切られ、以下のような意味を持つ。
- .jp – 国ドメイン(.uk イギリス,.ch 中国,アメリカは無し)
- .ac – 種別ドメイン(.co.jp,.com:会社,.ne.jp,net:ネットワーク系)
- fukui-nct – 組織ドメイン
- .ei. – サブドメイン(組織内が細分化されている場合)
- www. – ホスト名
このような省略されていない、対象となるコンピュータを指定するためのドメイン名は、FQDN(Fully Qualified Domain Name)と呼ばれる。
ただしアメリカでは、国ドメインを一般的に使わない。また最近では、世界的な企業では国ドメインが意味をなさないので、アメリカ以外でも .com や .net といった、トップレベルドメインが使われる。様々なサービスを展開している企業では、組織種別が意味をなさないため、toyota.jp といったものも増えてきた。
以下に、主要な組織ドメイン・国ドメインをあげる。
|
|
DNSのしくみ
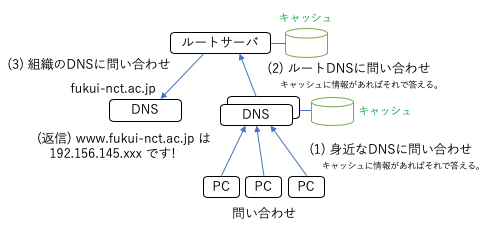
DNSは、Domain Name Service であり、コンピュータ名(ドメイン名)から、IPアドレスを調べるサービスで、ポート番号53,UDPを使っている。
インターネットに接続する際には、最も身近なDNSの情報が与えられ、ユーザがコンピュータ名を問い合わせると、身近なDNSがコンピュータのIPアドレスを返してくれる。この際に、検索結果はキャッシュとして一定期間保存される。身近なDNSがそのコンピュータ名を知らない場合は、上位のDNSに問い合わせを行い、DNSルートサーバもコンピュータ名をキャッシュしていない場合は、管理元の組織のDNSに問い合わせが行われる。
DNSと様々な情報
DNS では、様々な情報が取得できる。IPアドレス以外にも、メールを送ってもらうサーバのIPアドレス(MXレコード)なども取得できる。
DNSとセキュリティ
DNSは、コンピュータ名とIPアドレスを対応付けるものであり、これには正引き(コンピュータ名からIPアドレスを求める)と、逆引き(IPアドレスからコンピュータ名を求める)がある。セキュリティ対策が厳しい場所では、
- 正引きを使うことで、特定の組織のドメイン名を持つコンピュータからのアクセスを許可/禁止する。
- 正引きで、コンピュータ名が登録されている所からのみ許可する。
- IPアドレスから逆引きして求めたコンピュータ名をさらに正引きして同じIPアドレスが求まるかを確認
といった対策を行う。
- DNSのドメイン名は、当初は最初に申請した人に割り当てられる。このため、nintendo.com といったドメイン名を、関係ない人が取得するといったトラブルがあった。(サイバースクワッティング)
- DNSを用いたクラッキングでは、ウィルスに感染させたパソコンに偽物のIPアドレスを教えることで、偽装した別コンピュータに誘導し個人情報を盗む手口がある。(DNSポイズニング)
- 他にもウィルスに感染させた大量のパソコンから、同時にルートサーバに大量のDNSの問合せを送ることで、処理能力を低下させると、インターネット全体でDNS参照ができなくなる攻撃もある。(DNSルートサーバへの分散DoSアタック)
データベースの物理設計
最初にテストを返却した後、データベース物理設計の話を行う。来週はレポート課題作成日とすることから、課題を以下に示す。
データベース後半課題
データベース後半の課題は「卒業研究の対象をデータベースとして設計」とする。
情報系の卒研テーマであれば、処理対象のデータの中にはデータベースで管理するのがふさわしい対象について設計せよ。実験系の卒研テーマであれば、実験結果の表をデータベースで管理するとした場合の設計を行うこと。どちらでもない卒研で、卒研のテーマの中にデータベース化すべき対象が無い場合は、身の回りの帳票(例えばコンビニのレシートなど)をデータベース化することを検討すること。
レポートで記載する内容は、以下の通りとする。
- 卒業研究におけるデータベース化する対象の説明
- データベースをトップダウン設計する際の
- 実体と関連を抽出するまでの説明
- 正規化を行う経過の説明
- 上記を踏まえたトップダウン設計でのER図
- データベースをボトムアップ設計する際の
- 対象とする帳票に相当するデータの一例と説明
- レベル分けや正規化を行う経過の説明
- 上記を踏まえたボトムアップ設計でのER図
- 考察
- トップダウン設計とボトムアップ設計に違いがあれば、設計の見直しの過程の説明
- 両設計方法から分かったこと
データベースの物理設計
データベースの物理的設計は、データベースの格納法法や管理方法を決定する。この際には、ディスク容量の見積もりやメモリ量の見積もりが重要となる。
ディスク容量の見積もり
データベースでは、B木(以降で解説予定)などが用いられることが1つのB木のノード(データブロック)の構造をおおまかに示す。各データブロックには、そのブロックを管理するためのページ制御の情報と、実データへのポインタとなるスロット情報と、実データからなる。
実データは、すべてのデータが固定長であれば、そのデータ長とブロック毎のデータ数にページ制御の容量を加えれば良い。しかし、データ長は可変であることが多い。この場合は、データの更新でデータ長が長くなると、その後ろのデータをずらす処理が頻発すると、データ管理の効率が悪い。
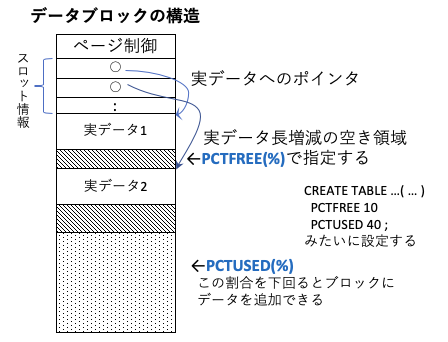
そこで、実データの間には、データ長が増えた時の空き領域を設けておく。この比率がPCTFREEと呼ばれ、この領域が埋まった時にのみデータをずらす処理を行う。
また、データベースへのデータの削除を行う場合、データが1つ消える度にデータブロックの構成を変化させると効率が悪く、通常はデータ削除の目印をつけるだけとすることが多い。データ削除で空きがふえた時だけ、データブロックの構成を変えたり、データ追加の際にデータを追加する。この比率は、PCTUSEDと呼ばれる。
このため、ハードディスク容量の見積もりでは、PCTFREE,PCTUSEDを考慮する必要がある。
一般的には、容量を減らす観点であれば、PCTFREEはなるべく小さく、PCTUSEDはなるべく大きい方が望ましいが、データの更新で追加・削除・修正が頻発するのであれば、PCTFREEはある程度大きく、PCTUSEDはある程度小さい方がよい。このため、PCTFREE+PCTUSED < 100 となるようにチューニングすることが多い。
また、実際のデータとは別に、データを高速に検索するためのインデックスファイルが作られるので、この容量も別途考慮が必要となる。
補足:残り予定:トランザクション処理, 内部構造, テスト前レポート課題
ハッシュ法(導入)
前半は中間試験の返却と解説を行う。後半は次のテーマのハッシュ法の導入話。
ここまでの授業では、配列(データ検索は、登録順保存ならO(N)、2分探索ならO(log N)となる、2分探索ができるのは配列がランダムアクセスができるからこそ)、単純リスト(データ検索(シーケンシャルアクセスしかできないのでO(N)となる)、2分探索木( O(log N) ) といった手法を説明してきた。しかし、もっと高速なデータ検索はできないのであろうか?
究極のシンプルなやり方(メモリの無駄)
最も簡単なアルゴリズムは、電話番号から名前を求めるようなデータベースであれば、電話番号自身を配列添え字番号とする方法がある。しかしながら、この方法は大量のメモリを必要とする。
// メモリ無駄遣いな超高速方法
struct PhoneName {
int phone ;
char name[ 20 ] ;
} ;
// 電話番号は6桁とする。
struct PhoneName table[ 1000000 ] ; // 携帯電話番号ならどーなる!?!?
// 配列に電話番号と名前を保存
void entry( int phone , char* name ) {
table[ phone ].phone = phone ;
strcpy( table[ phone ].name , name ) ;
}
// 電話番号から名前を調べる
char* search( int phone ) {
return table[ phone ].name ;
}
しかし、50人程度のデータであれば、電話番号の末尾2桁を取り出した場合、同じ数値の人がいることは少ないであろう。であれば、電話番号の末尾2桁の値を配列の添え字番号として、データを保存すれば、配列サイズは100件となり、メモリの無駄を減らすことができる。
ハッシュ法
先に述べたように、データの一部を取り出して、それを配列の添え字番号として保存することで、高速にデータを読み書きできるようにするアルゴリズムはハッシュ法と呼ばれる。データを格納する表をハッシュ表、データの一部を取り出した添え字番号はハッシュ値、ハッシュ値を得るための関数がハッシュ関数と呼ばれる。
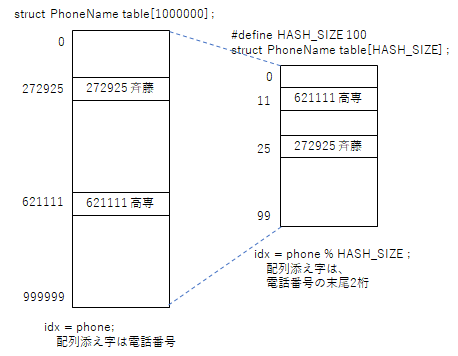
// ハッシュ衝突を考えないハッシュ法
#define HASH_SIZE 100 ;
struct PhoneName table[ HASH_SIZE ] ;
// ハッシュ関数
int hash_func( int phone ) {
return phone % HASH_SIZE ;
}
// 配列に電話番号と名前を保存
void entry( int phone , name ) {
int idx = hash_func( phone ) ;
table[ idx ].phone = phone ;
strcpy( table[ idx ].name , name ) ;
}
// 電話番号から名前を調べる
char* search( int phone ) {
int idx = hash_func( phone ) ;
return table[ idx ].name ;
}
ただし、上記のプログラムでは、電話番号の末尾2桁が偶然他の人と同じになることを考慮していない。
例えば、データ件数が100件あれば、同じ値の人も出てくるであろう。このように、異なるデータなのに同じハッシュ値が求まることを、ハッシュ衝突と呼ぶ。
たとえ話で言うなら、100個の椅子が連番付きで並んでいて、自分の電話番号末尾2桁の場所に座ろうとしたら、先に座っている人がいるような状態である。このような状態で、あなたなら何処に座るだろうか?
ハッシュ関数に求められる特性
ハッシュ関数は、できる限り同じような値が求まるものは、ハッシュ衝突が多発するので、避けなければならない。例えば、6桁の電話番号の先頭2桁であれば、電話番号の局番であり、同じ学校の人でデータを覚えたら、同じ地域の人でハッシュ衝突が発生してしまう。また、ハッシュ値を計算するのに、配列の空き場所を一つ一つ探すような方式では、データ件数に比例した時間がかかり、高速なアルゴリズムでなくなってしまう。このことから、ハッシュ関数には以下のような特徴が必要となる。
- 同じハッシュ値が発生しづらい(一見してデタラメのように見える値)
- 簡単な計算で求まること。
- 同じデータに対し常に、同じハッシュ値が求まること。
理解度確認・小テスト
11/23は前回未消化ネタの説明とテスト対策
11/23の授業は、前回の「トランスポート層・TCPとUDP」の未消化分の説明と、過去の試験問題の自主勉強時間。




