リスト処理
リスト構造
リスト構造は、データと次のデータへのポインタで構成され、必要に応じてメモリを確保することで、配列の上限が制限にならないようにする。また、次のデータへのポインタでつなげているため、途中へのデータ挿入が簡単にできるようにする。
まずは、メモリ確保とポインタをつなげるイメージを確実に理解してもらうために、1つ1つのデータをポインタでつなげる処理を示す。
#include <stdio.h>
#include <stdlib.h>
// List構造の宣言
struct List {
int data ; // データ保存部
struct List* next ; // 次のデータへのポインタ
} ;
int main() {
struct List* top ; // データの先頭
struct List* p ;
// (1)
top = (struct List*)malloc( sizeof( struct List ) ) ;
top->data = 111 ;
// (2)
top->next = (struct List*)malloc( sizeof( struct List ) ) ;
top->next->data = 222 ;
// (3)
top->next->next = (struct List*)malloc( sizeof( struct List ) ) ;
top->next->next->data = 333 ;
top->next->next->next = NULL ; // 末尾データの目印
for( p = top ; p != NULL ; p = p->next ) {
printf( "%d¥n" , p->data ) ;
}
return 0 ;
}
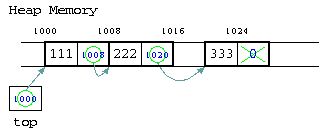
 このようなメモリーの中のポインタの指し示す番地のイメージを、具体的な番地の数字を書いてみると、以下のような図で表せる。先頭の111が入った部分が1000番地であったなら、topというポインタには1000番地が入っている。
このようなメモリーの中のポインタの指し示す番地のイメージを、具体的な番地の数字を書いてみると、以下のような図で表せる。先頭の111が入った部分が1000番地であったなら、topというポインタには1000番地が入っている。
NULLって何?
前回の授業で説明した、次の配列の添え字の番号を使う方式では、データの末尾を示すためには、-1 を使った。-1 は、配列の添え字で通常ありえない値であり、次のデータはないという目印とした。
同じように、C言語では、通常あり得ないポインタとして、0 番地を示す NULL が定義されている。
#define NULL 0
補助関数
上記のプログラムでは、(struct…)malloc(sizeof(…))を何度も記載し、プログラムが分かりにくいので、以下に示す補助関数を使うと、シンプルに記載できる。
struct List* cons( int x , struct List* n ) {
struct List* ans ;
ans = (struct List*)malloc( sizeof( struct List ) ) ;
if ( ans != NULL ) {
ans->data = x ;
ans->next = n ;
}
return ans ;
}
int main() {
struct List* top ;
top = cons( 111 , cons( 222 , cons( 333 , NULL ) ) ) ;
:
return 0 ;
}
補助関数の名前の cons は、constructor の略であり、古くから使われている List Processor(LISP)※ というプログラム言語でのリスト(セル)を生成する関数が cons 。
typedefを使った書き方
List構造の宣言は、古い書き方では typedef を使うことも多い。typedef は、型宣言において新しい型の名前をつける命令。
// typedef の使い方 // typedef 型宣言 型名 ; typedef unsigned int uint32 ; // 符号なし32bit整数をシンプルに書きたい uint32 x = 12345 ; typedef struct LIST { // 構造体のタグ名と新しくつける型名と重複できない int data ; // のでこの時点のタグ名は "LIST" としておく struct LIST* next ; } List ; List* cons( int x , List* n ) { // C++なら struct List { ... } ; と書く List* ans ; // だけでこういう表記が可能 ans = (List*)malloc( sizeof( List ) ) ; : ((略)) } int main() { List* top ; top = cons( 111 , cons( 222 , cons( 333 , NULL ) ) ) ; : ((略)) }最近のC言語(C++)では、構造体のタグ名がそのまま型名として使えるので、こういう書き方をする必要はなくなってきている。
// 最近のC++なら... struct List { public: int data ; List* next ; public: List( int x , List* n ) : data( x ) , next( n ) {} } ; int main() { List* top = new List( 1 , new List( 2 , new List( 3 , NULL ) ) ) ; : }LISP※と関数型プログラミング言語
LISPの歴史は長く、最古のFORTRAN,COBOLに次ぐ3番目ぐらいに遡る。最初は、人工知能※※(AI)のプログラム開発のための関数型プログラミング言語として作られた。特徴として、データもプログラムもすべてリスト構造(S式)で表すことができ、プログラムは関数型に基づいて作られる。
関数型プログラミングは、Ruby や Python でも取り入れられている。関数型プログラミングは、処理を関数をベースに記述することで「副作用を最小限にすることができ」、極端な話をすればループも再帰呼出しの関数で書けばいい…。
LISPの処理系は、最近では Scheme などが普通だが、プログラムエディタの Emacs は、内部処理が LISP で記述されている。
古いAI※※と最近のAIの違い
最近では、AI(Artificial Intelligence) という言葉が復活してきたが、LISP が開発された頃の AI と最近注目されている AI は、微妙に異なる点がある。
LISPが開発された頃の AI は、関数型のプログラム言語で論理的思考を表現することが目標であった。頭脳を左脳と右脳の違いで表現することが多いが、どちらかというと「分析的で論理的に優れ、言語力や計算機能が高い」とされる左脳を作り出すようなもの。しかしながら、この時代では、漠然としたパターンを認識したりするような「感覚的、直感的な能力に優れ総合判断力を司る右脳」のような処理は苦手であった。
しかしながら、最近注目されている AI は、脳神経を真似たニューラルネットワークから発展した機械学習やディープラーニングという技法により今まで難しかった右脳の機能を実現することで、左脳と右脳の機能を兼ね備えたものとなっている。
将棋のプログラミングで例えるなら、左脳(古いAI)に例えられるのが正確に先の手を読む機能であり、右脳に例えられる機能が大局観(全体の良し悪しを見極める判断能力)といえる。
簡単なリスト処理の例
先に示したリスト構造について簡単なプログラム作成を通して、プログラミングに慣れてみよう。
// 全要素を表示する関数
void print( struct List* p ) {
for( ; p != NULL ; p = p->next )
printf( "%d " , p->data ) ;
printf( "¥n" ) ;
}
// データ数を返す関数
int count( struct List* p ) {
int c = 0 ;
for( ; p != NULL ; p = p->next )
c++ ;
return c ;
}
int main() {
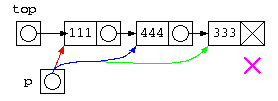
struct List* top = cons( 111 , cons( 444 , cons( 333 , NULL ) ) ) ;
print( top ) ;
printf( "%d¥n" , count( top ) ) ;
return 0 ;
}
リスト処理を自分で考えて作成
以下のようなプログラムを作ってみよう。意味がわかって慣れてくれば、配列の部分の for の回し方が変わっただけということに慣れてくるだろう。
// 全要素の合計
int sum( struct List* p ) {
// sum( top ) → 888
自分で考えよう
}
// リストの最大値を返す
int max( struct List* p ) {
// max( top ) → 444 (データ件数0の場合0を返す)
自分で考えよう
}
// リストの平均値を返す
double mean( struct List* p ) {
// (111+444+333)/3=296.0
自分で考えよう
}
// リストの中から指定した値の場所を返す
int find( struct List* p , int key ) {
// find( top , 444 ) = 1 (先頭0番目)
// 見つからなかったら -1
自分で考えよう
}
再帰呼び出しでリスト処理
リスト処理の応用のプログラムを作るなかで、2分木などのプログラミングでは、リスト処理で再帰呼出しを使うことも多いので、先に示したプログラムを再帰呼び出しで書いたらどうなるであろうか?
// 全データを表示
void print( struct List* p ) {
if ( p == NULL ) {
printf( "¥n" ) ;
} else {
printf( "%d " , p->data ) ;
print( p->next ) ; // 末尾再帰
}
}
// データ数を返す関数
int count( struct List* p ) {
if ( p == NULL )
return 0 ;
else
return 1 + count( p->next ) ; // 末尾再帰
}
// 全要素の合計
int sum( struct List* p ) {
// sum( top ) → 888
自分で考えよう
}
// リストの最大値を返す
int max( struct List* p ) {
// max( top ) → 444 (データ件数0の場合0を返す)
自分で考えよう
}
// リストの中から指定した値を探す。
int find( struct List* p , int key ) {
// find( top , 444 ) = 1
// 見つかったら1 , 見つからなかったら 0
自分で考えよう
}
理解度確認
上記プログラム中の sum() , max() , find() を再帰呼び出しをつかって記述せよ。
その他の構造図と振る舞い図
前回の講義で説明した構造図について、クラス図・オブジェクト図以外について改めて説明と、振る舞い図の説明。
構造図
構造図の主なものとして、クラス図、オブジェクト図以外に、
- パッケージ図(クラスなどをグループ化したパッケージの関係)
- コンポジット構造図(クラスやコンポーネントの内部構造を示す)
- コンポーネント図(コンポーネントの内部構造とコンポーネント間の依存関係)
- 配置図(システムの物理的な構成)
パッケージ図
パッケージ図は、クラス図をパッケージ毎に分類して記載する図。 パッケージのグループを、フォルダのような図で記載する。

IT専科から引用
コンポーネント図とコンポジット構造図
コンポジット構造図は、クラスやコンポーネントの内部構造を示すもので、コンポーネント図は、複数のクラスで構成される処理に、 インタフェースを用意し、あたかも1つのクラスのように扱ったもの。 接続するインタフェースを飴玉と飴玉を受けるクチのイメージで、提供側を◯───で表し、要求側を⊃──で表す。
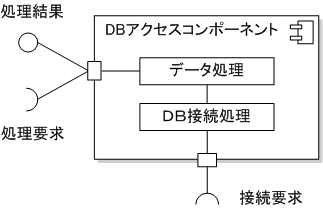
IT専科から引用
配置図
配置図は、システムのハードウェア構成や通信経路などを表現するための図。 ハードウェアは直方体の絵で表現し、 デバイスの説明は、”≪device≫”などを示し、実行環境には、”≪executionEnvironment≫” などの目印で表現する。
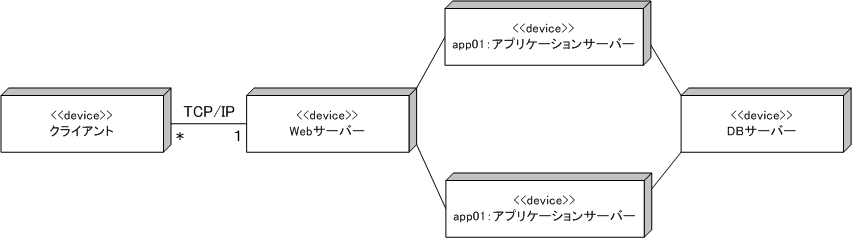
IT専科から引用
振る舞い図
参考資料図をもとに振る舞い図の説明を行う。
ユースケース図

ユーザなど外部からの要求に対する、システムの振る舞いを表現するための活用事例や機能を表す図がユースケース図。 システムを構築する際に、最初に記述するUMLであり、システムに対する処理要件の全体像や機能を理解するために記述する。 ユーザや外部のシステムは、アクターとよび人形の絵で示す。楕円でシステムに対する具体的な処理をユースケースとして楕円で記述する。 関連する複数のユースケースをまとめて、サブジェクトとして示す場合もある。
アクティビティ図
処理順序を記述するための図にはフローチャートがあるが、上から下に処理順序を記述するため、縦長の図になりやすい。また、四角枠の中に複雑なことを書けないので、UMLではアクティビティ図を用いる。
初期状態●から、終了状態◉までの手順を示すためのものがアクティビティ図。 フローチャートに無い表現として、複数の処理を並行処理する場合には、フォークノードで複数の処理を併記し、最終的に1つの処理になる部分をマージノードで示す。 通常の処理は、角丸の長方形で示し、条件分岐はひし形で示す。
ステートチャート図(状態遷移図)
ステートチャート図は、処理内部での状態遷移を示すための図。 1つの状態を長丸長方形で示し、初期状態●から終了状態◉までを結ぶ。 1つの状態から、なんらかの状態で他の状態に遷移する場合は、分岐条件となる契機(タイミング)とその条件、およびその効果(出力)を「契機[条件]/効果」で矢印に併記する。 複数の状態をグループ化して表す場合もある。
シーケンス図
複数のオブジェクトが相互にやり取りをしながら処理が進むようなもののタイミングを記述するためのものがシーケンス図。 上部の長方形にクラス/オブジェクトを示し、その下に縦軸にて時系列の処理の流れの線(Life Line)を描く。 オブジェクトがアクティブな状態は、縦長の長方形で示し、そのLife Line間を、やり取り(メッセージ)の線で相互に結ぶ。 メッセージは、相手側からの返答を待つような同期メッセージは、黒塗り三角矢印で示す。 返答を待たない非同期メッセージは矢印で示し、返答は破線で示す。
コミュニケーション図
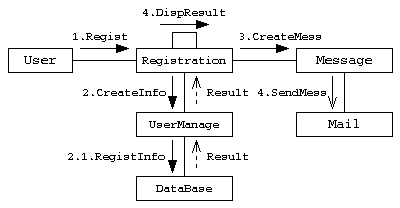
クラスやオブジェクトの間の処理とその応答(相互作用)と関連の両方を表現する図。
応答を待つ同期メッセージは -▶︎、非同期メッセージは→で表す。複数のオブジェクト間のやりとりの相互作用を表現する。
D/A・A/D変換回路と誤差
小型コンピュータを使った制御では、外部回路に指定した電圧を出力(D/A変換)したり、外部の電圧を入力(A/D変換)したりすることが多い。以下にその為の回路と動作について説明する。
D/A変換回路
ラダー抵抗回路によるD/A変換の仕組みを引用
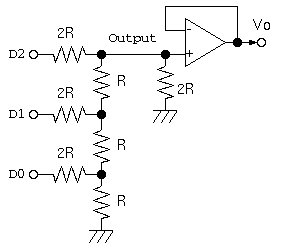
このような回路で、D0,D1,D2 は、デジタル値の0=0[V] , 1=5[V] であった場合、Output 部分の電圧は、(D0,D1,D2)の値が、(0,0,0),(0,0,1),…(1,1,1)と変化するにつれ、5/8[V]づつ増え、(1,1,1)で 5*(7/8)=4.4[V]に近づいていく。Output が出力によって電圧が変化しないように、アンプ回路を通す。
DCモータをアナログ量で制御しないこと
このように、電圧をコンピュータから制御するようになると、ロボットで模型用の直流モータの回転速度をこれで制御したい…と考えるかもしれない。
しかし、直流モータは、ブラシとコイル(電磁石)を組み合わせたものだが、モーターが回転しだす瞬間でみれば、コイルは単なる導線である。このため、小さい電流でゆっくりモータを回転させようとすると、たとえ小さい電圧でも導線(抵抗はほぼ0[Ω])には大量の電流が流れ、モータをスイッチングする回路は焼き切れるかもしれない。
PWM変調
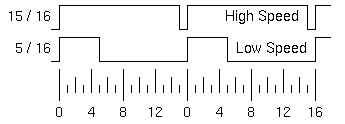
こういう場合には、PWM変調(Pulse Width Modulation) を行う。電圧の高さは一定で、高速回転させるときは長時間電圧をONにするが、低速回転させるときはONとOFFを繰り返し信号でONの時間を短くする。
このような波形であれば、低速度でも電流が流れる時間が短く、大量の電流消費は避けられ、モーターをまわす力も安定する。
A/D変換回路
D/A変換とは逆に、アナログ量をデジタル値に変換するには、どのようにするか?
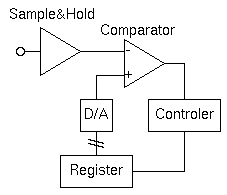
このような場合には、A/D変換回路を用いる。一般的な回路では、以下のような逐次比較型A/D変換を用いる。
この回路では、変換開始と共に入力値をサンプル保持回路でアナログ量を保存する。
その後、Registerの中のデジタル値を、D/A 変換回路でアナログ量に変換した結果を、比較器(Comparator)でどちらが大きいか判断し、その結果に応じて2分探索法とかハイアンドローの方式のように、比較を繰り返しながらデジタル値を入力値に近づけていく。
ハイアンドロー(数あてゲーム)
数あてゲームで、デタラメな0〜127までの整数を決めて、ヒントを元にその数字を当てる。回答者は、数字を伝えると、決めた数よりHighかLowのヒントをもらえる。
最も速い回答方法は…例えば決めた数が55だとすると
・初期状態 ??????? 0..127 ・64 - Low 0?????? 0..63 ・32 - High 01????? 32..63 ・48 - High 011???? 48..63 ・56 - Low 0110??? 48..55 ・52 - High 01101?? 52..55 ・54 - High 011011? 54..55 ・55 - Bingo 0110111 55確定どんな値でも、7回(27=127)までで当てることができる。
量子化と量子化誤差
アナログデータ(連続量)をデジタルデータなどの離散的な値で近似的に表すことを、量子化という。
量子化誤差とは、信号をアナログからデジタルに変換する際に生じる誤差のことをいう。
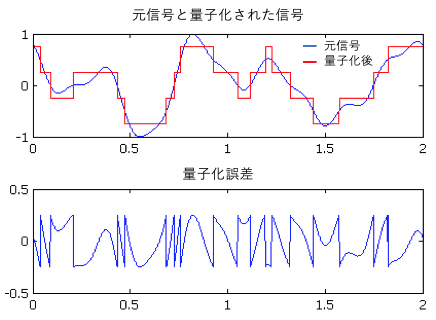
アナログ信号からデジタル信号への変換を行う際、誤差は避けられない。アナログ信号は連続的で無限の正確さを伴うが、デジタル信号の正確さは量子化の解像度やアナログ-デジタル変換回路のビット数に依存する。
偶然誤差
アナログ信号がA/D変換回路に入るまでに、アナログ部品の電気的変動(ノイズ)が原因で値が変動することもある。ノイズが時間的に不規則に発生し、値が増えてしまったり減ってしまったり偶然に発生するものは偶然誤差という。偶然誤差を加えると相殺されてほぼ0になるのであれば、統計的な手法で誤差の影響を減らすことができる。
数値と誤差
コンピュータで計算すると、計算結果はすべて正しいと勘違いをしている人も多い。ここで、改めて誤差について考える。
特に、A/D変換したような値であれば、値自体に誤差が含まれている。
こういった誤差が含まれる数字を扱う場合注意が必要である。例えば、12.3 と 12.300 では意味が異なる。測定値であやふやな桁を丸めたのであれば、前者は 12.25〜12.3499 の間の値であり有効数字3桁である。後者は、12.2995〜12.300499 の間の値であり、有効数字5桁である。このため、誤差が含まれる数字の加算・減算・乗算・除算では注意が必要である。
加減乗除算の場合
加減算であれば小数点の位置を揃え、誤差が含まれる桁は有効桁に含めてはいけない。

上記の計算では、0.4567の0.0567の部分は意味がないデータとなる。(情報落ち)
乗除算であれば、有効桁の少ない値と有効桁の多い値の計算では、有効桁の少ない方の誤差が計算結果に出てくるため、通常は、有効桁5桁と2桁の計算であれば、乗除算結果は少ない2桁で書くべきである。

桁落ち
有効桁が大きい結果でも、減算が含まれる場合は注意が必要である。
例えば、以下のような計算では、有効桁7桁どうしでも、計算結果の有効桁は3桁となる。

このような現象は、桁落ちと呼ばれる。
なぜデジタル信号を使うのか
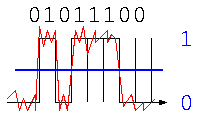
コンピュータが信号処理でなぜ使われるのか?例えば、下の信号のように、電圧の低い/高いで0/1を表現したとする。
ノイズが混入しづらい
このデータ”01011100″を通信相手に送る場合、通信の途中でノイズ(図中の赤)のような信号が加わった場合、アナログ信号では、どれがノイズなのか判別することはできない。しかしデジタル信号であれば、真ん中青線より上/下か?で判別すれば、ノイズの影響は無視して、元どおりの”01011100″を取り出せる。この0か1かを判別するための区切り(図中青線)は、しきい値と呼ばれる。
ノイズを見つける・治す
また、”01011100″のデータを送る通信の途中で、しきい値を越えるようなノイズが混ざって、受信したとする。この場合、単純に受け取るだけであれば、”01010100″で間違った値を受け取っても判別できない。しかし、データを送る際にパリティビット(偶数パリティであれば全データの1の数が偶数になるように)1ビットのデータを加える。このデータを受け取った際に、ノイズで1ビット反転した場合、1の数が奇数(3個)なので、ノイズでビット反転が発生したことがわかる。これをパリティチェックと言う。
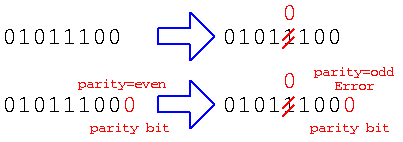
このように、デジタル信号を使えば、しきい値を越えない程度のノイズならノイズの影響を無視できるし、たとえ大きなノイズでデータに間違いがあっても、パリティチェックのような方法を使えば間違って伝わったことを判別できる。
パリティチェックは、元のデータに1bitの信号を追加することで誤り検出ができるが、2bit同時に変化してしまうと誤りを見つけられない。そこで、元データにさらに多くのbit情報を追加すると、1bitの間違いを元に戻すようにもできる。誤り検出・訂正
電子回路で制御するかコンピュータで制御するか
これ以外にも、デジタル信号にする理由がある。
アナログ回路(電子回路)で制御しようとすると、抵抗やコイルやコンデンサといった受動素子が必要となるが、その中でもコイルは小型化がしづらい部品で、制御回路全体の小型化が難しい。大量生産ができるような回路なら小型化ができるかもしれないが、多品種少量の生産物では小型化のための開発費用の元がとれない。しかし、大量生産された安価な小型コンピュータで制御すれば、制御回路全体の小型化も可能となる。
また、電子回路の特性を調整するには、抵抗などの部品をはんだ付けをしながら部品を交換することになるかもしれない。しかしながら、アナログ信号をデジタル信号にしてしまえば、ノイズを減らすための平均化処理などは計算で実現できるし、特性を変化させるための調整もプログラムの数値を変更するだけで可能となる。