B木とデータベース
2分探索木の考え方を拡張したもので、B木がある。
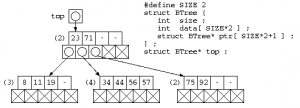
B木の構造
2分木では、データの増減で木の組換えの発生頻度が高い。そこで、1つのノード内に複数のデータを一定数覚える方法をとる。B木では、位数=Nに対し、最大2N個のデータd0..d2N-1と、2N+1本のポインタp0..p2Nから構成される。piの先には、di-1<x<di を満たすデータが入った B木のノードを配置する。ただし、データの充填率を下げないようにするため、データは最小でもN個、最大で2N個を保存する。
B木からデータの検索
データを探す場合は、ノード内のデータ diの中から探し、見つからない場合は、ポインタの先のデータを探す。位数がある程度大きい場合、ノード内の検索は2分探索法が使用できる。また、1つのノード内の検索が終われば、探索するデータ件数は、1/N〜1/2Nとなることから、指数的に対象件数が減っていく。よって、検索時間のオーダは、O(logN) となる。
B木へのデータの追加
B木にデータを追加する場合は、ノード内に空きがあれば、単純にデータの追加を行う。ノード内のデータが2N個を越える場合は、以下のような処理を行う。
ノード内のデータと追加データを並べ、その中央値を選ぶ。この中央値より大きいデータは、新たにつくられたノードに移す。中央値のデータは上のノードに追加処理を行う。このような方法を取ることで、2分木のような木の偏りが作られにくい構造となるようにする。
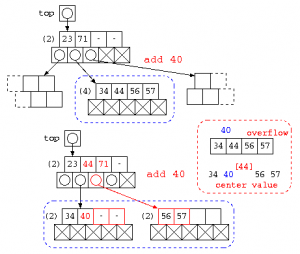
データを削除する場合も同様に、データ件数がN個を下回る場合は、隣接するノードからデータを取ってくることで、N個を下回らないようにする。
B木とデータベース
このB木の構造は、一般的にデータベースのデータを保存するために広く利用されている。
データベースシステムでは、データを効率よく保存するだけでなく、データの一貫性が保たれるように作られている。
例えば、データベースのシステムが途中でクラッシュした場合でも、データ更新履歴の情報を元にデータを元に戻し、データを再投入して復旧できなければならない。データを複数の所からアクセスした場合に、その順序から変な値にならないように、排他制御も行ってくれる。
データベースで最も使われているシステムは、データすべてを表形式で扱うリレーショナル・データベースである。
((リレーショナル・データベースの例)) STUDENT RESULT ID | name | grade | course ID | subject | point -----+----------+-------+-------- -----+---------+------- 1001 | t-saitoh | 5 | EI 1001 | math | 83 1002 | sakamoto | 4 | E 1001 | english | 65 1003 | aoyama | 4 | EI 1002 | english | 90 ((SQLの例)) select STUDENT.name , RESULT.subject , RESULT.point --射影-- from STUDENT , RESULT --結合-- where STUDENT.ID == RESULT.ID -- 串刺し -- --選択-- and RESULT.point >= 60 ; ((上記SQLをC言語で書いた場合)) for( st = 0 ; st < 3 ; st++ ) // 結合 for( re = 0 ; re < 3 ; re++ ) if ( student[ st ].ID == result[ re ].ID // 選択 && result[ re ].point >= 60 ) printf( "%s %s %d" , // 射影 student[ st ].name , result[ re ].subject , result[ re ].point ) ;
B+木
データベースの処理では、目的のデータを O(log N) で見つける以外にも、全データに対する処理も重要である。この場合、全てのデータに対する処理では、単純なB木では再帰呼び出しが必要となる。しかし、他の表でも再帰処理を伴うと、プログラムは複雑になってしまう。
そこで、B木のデータを横方向に並べて処理を行う場合に、その処理が簡単になるように B+木が用いられる。
この方法では、末端のノードは、隣接するノードへのポインタを持つ。

Wikipedia B+木 より引用
JavaScriptの再帰の例題
再帰呼び出しで分割統治法の考え方のプログラムをJavaScriptで書いたサンプル
単純に、配列の指定範囲の合計を求める関数を、再帰を用いて記述する。
<html>
<head>
</head>
<body>
<p>
このプログラムは、実行結果を console.log() で出力するので、
Ctrl+Shift+I で、JavaScript の console を表示させてね。
</p>
<script type="text/javascript">
// a : 配列
// start : 合計を計算する範囲の戦闘
// end : 合計を計算する範囲の最後+1
// 配列の合計は、配列の先頭 + 残りの合計
function array_sum( a , start , end ) {
console.log( "array_sum:" + start + "," + end ) ;
if ( start == end ) {
console.log( "array_sum(" + start + "," + end + ")=0" ) ;
return 0 ;
} else {
var ans = a[ start ] + array_sum( a , start + 1 , end ) ;
console.log( "array_sum("+start+","+end+")="+ans ) ;
return ans ;
}
}
var array = new Array( 11 , 22 , 33 , 44 , 55 , 66 , 77 , 88 ) ;
console.log( array_sum( array , 0 , array.length ) ) ;
// 配列の合計は、データが1個ならその値。
// そうでなければ、配列の前半の合計 + 配列の後半の合計
function array_sum2( a , start , end ) {
console.log( "array_sum2:" + start + "," + end ) ;
if ( start + 1 == end ) {
var ans = a[ start ] ;
console.log( "array_sum2("+start+","+end+")="+ans ) ;
return ans ;
} else {
var mid = Math.floor( ( start + end ) / 2 ) ;
var ans = array_sum2( a , start , mid ) // 配列前半の合計を求める
+ array_sum2( a , mid , end ) ; // 配列後半の合計を求める
console.log( "array_sum2("+start+","+end+")="+ans ) ;
return ans ;
}
}
console.log( array_sum2( array , 0 , array.length ) ) ;
</script>
</body>
</html>
データベースの設計と正規形
適切でないデータベースを例にしながら、更新不整合が発生することを説明する。 (不整合には、修正不整合・挿入不整合・削除不整合がある。) この不整合が発生しないデータベース(表)を作るためには、どうすべきかを解説。
ERモデル
不整合が起こらないようなデータベースとするには、実体と関連にモデル化を行う。 実体・関連には、属性(attribute)が付随し、実体を長方形、関連をひし形、属性を楕円で表現する ER図を描く。

学生や教員といった実体は、人という汎化した視点であれば、識別番号と名前の属性で 表現できると意味で、共通である。人を学生という視点で特化した先に、学科名や学年といった 属性を持つと考えられる。こういった汎化階層は、オブジェクト指向と同じ。
実体の中には、他の実体と関連を持って初めて意味を持つ実体もある。 関連先の実体が消えれば、存在自体が無意味になってしまう実体は、弱実体と呼ぶ。
正規形
データベースにおいて、様々な不整合を防ぐために正しい設計が必要であることを 改めて説明し、それには正規形としての条件を満たしている必要があることを説明する。
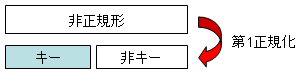
第一正規形は、すべての要素が原子値である条件を満たせばいい。 要素の中が複数の項目であったり表形式のデータがあると、 表構造のリレーショナルデータベースにはできない。
キーの説明:超キー(スーパーキー)とは、データベースで1つのデータを 選び出すために必要なデータ項目であり、複数の項目で1データを指定 できる場合もある。
候補キーとは、必要最小限の項目となっているものを指す。 1項目が抜けても選別できなくなるようであれば、候補キーとは言わない。 主キーとは、候補キーのなかで管理の都合上便利なもの。
データ項目の値が決まると、他のデータ項目が自動的に決まるものは、 従属関係があるという。
 |
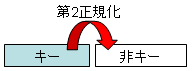 |
| 第1正規化 | 第2正規化 |
第二正規形は、部分従属がなく、すべての非キーデータ項目が、候補キーに 完全従属する場合をいう。
完全従属とは、候補キーを構成する全てのデータ項目に、非キーデータ項目が従属していること。 部分従属とは、候補キーを構成するデータ項目の一部のデータ項目に、非キー項目が従属していること。
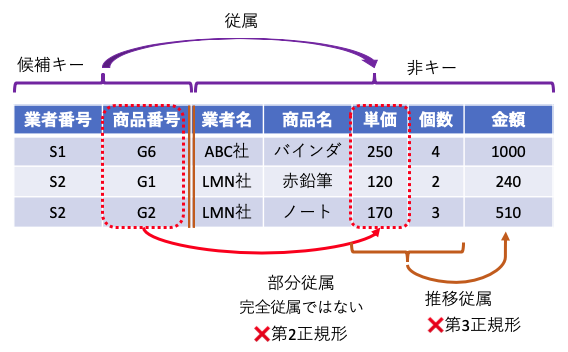
この例において、単価は商品が決まれば自動的に求まる情報。 (単価が日々変化することはないという条件で…) これは、部分従属となる。
推移従属性とは、データ項目でA→B→Cと、次々と値が求められる関係を指す。 このなかで、第三正規形とは、 候補キー以外の非キーデータ項目は、候補キーに完全従属し、 かつどの候補キーにも推移従属しない関係をいう。
 |
| 第3正規化 |
上記の例では、単価と個数が決まれば、金額が求まる推移従属の関係が含まれている。
おまけ:BC正規形,第4,5正規形
この他にも、 さらに非キーからキーに関数従属性がある場合にそれを取り除く、 ボイスコッド正規形(BC正規化)。 「対称性のある多値従属性(キーを決めると複数データが該当)」を分解して得られる第4正規形や、 「元になるテーブルの結合従属性を維持して分解することにより得られる第5正規形などがある。