ホーム » 「deque」タグがついた投稿
タグアーカイブ: deque
双方向リスト
リスト構造の利点と欠点
リストを使った集合演算のように、データを連ねたリストは、単純リストとか線形リストと呼ばれる。特徴はデータ数に応じてメモリを確保する点や、途中へのデータの挿入削除が得意な点があげられる。一方で、配列は想定最大データ件数で宣言してしまうと、実際のデータ数が少ない場合、メモリの無駄も発生する。しかし、想定件数と実データ件数がそれなりに一致していれば、無駄も必要最小限となる。リスト構造では、次のデータへのポインタを必要とすることから、常にポインタ分のメモリは、データにのみ注目すれば無駄となる。
例えば、整数型のデータを最大 MAX 件保存したいけど、実際は それ以下の、平均 N 件扱うとする。この時のメモリの使用量 M は、以下のようになるであろう。
| 配列の場合 | リスト構造の場合 |
(ただしヒープ管理用メモリ使用量は無視) |
シーケンシャルアクセス・ランダムアクセス
もう1つの欠点がシーケンシャルアクセスとなる。テープ上に記録された情報を読む場合、後ろのデータを読むには途中データを読み飛ばす必要があり、データ件数に比例したアクセス時間を要する。このような N番目 データ参照に、O(N)の時間を要するものは、シーケンシャルアクセスと呼ばれる。
一方、配列はどの場所であれ、一定時間でデータの参照が可能であり、これは ランダムアクセスと呼ばれる。N番目のアクセス時間がO(1)を要する。
このため、プログラム・エディタの文字データの管理などに単純リストを用いた場合、1つ前の行に移動するには、先頭から編集行までの移動で O(N) の時間がかかり、大量の行数の編集では、使いものにならない。ここで、シーケンシャルアクセスでも1つ前にもどるだけでも処理時間を改善してみよう。
単純リストから双方向リストへ
ここまで説明してきた単純リストは、次のデータへのポインタを持つ。ここで、1つ後ろのデータ(N番目からN+1番目)をアクセスするのは簡単だけど、1つ前のデータ(N-1番目)を参照しようと思ったら、先頭から(N-1)番目を辿るしかない。でも、これは O(N) の処理であり時間がかかる処理。
ではどうすればよいのか?
この場合、一つ前のデータの場所を覚えているポインタがあれば良い。
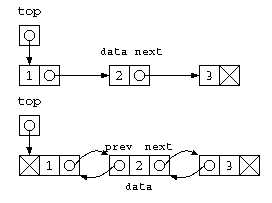
// 双方向リストの宣言
struct BD_List {
struct BD_List* prev ; // 1つ前のデータへのポインタ
int data ;
struct BD_List* next ; // 次のデータへのポインタ
} ;
このデータ構造は、双方向リスト(bi-directional list)と呼ばれる。
双方向リストは以前は、プログラムのエディタなどを実装する場合によく使われていた。エディタであれば、1つ前の行や次の行を参照することが多いため。しかし、最近では単純な双方向リストでエディタを実装することはない。
では、簡単なプログラムを書いてみよう。双方向リストのデータを簡単に生成するための補助関数から書いてみる。
// リスト生成補助関数
struct BD_List* bd_cons( struct BD_List* p ,
int d ,
struct BD_List* n ) {
struct BD_List* ans ;
ans = (struct BD_List*)malloc(
sizeof( struct BD_List ) ) ;
if ( ans != NULL ) {
ans->prev = p ;
ans->data = d ;
ans->next = n ;
}
return ans ;
}
void main() {
struct BD_List* top ;
struct BD_List* p ;
// 順方向のポインタでリストを生成
top = bd_cons( NULL , 1 ,
bd_cons( NULL , 2 ,
bd_cons( NULL , 3 , NULL ) ) ) ;
// 逆方向のポインタを埋める
top->next->prev = top ;
top->next->next->prev = top->next ;
// リストを辿る処理
for( p = top ; p->next != NULL ; p = p->next )
printf( "%d\n" , p->data ) ;
for( ; p->prev != NULL ; p = p->prev )
printf( "%d\n" , p->data ) ;
}
双方向リストの関数作成
以上の説明で、双方向の基礎的なプログラムの意味が分かった所で、練習問題。
先のプログラムでは、1,2,3 を要素とするリストを、ナマで記述していた。実際には、どんなデータがくるか分からないし、指定したポインタ p の後ろに、データを1件挿入する処理 bd_insert( p , 値 ) , また、p の後ろのデータを消す処理 bd_delete( p ) を書いてみよう。
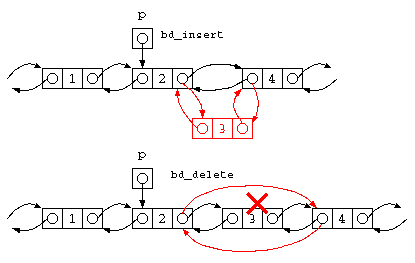
// 双方向リストの指定場所 p の後ろに、値 d を要素とするデータを挿入せよ。
void bd_insert( struct BD_List* p , int d ) {
struct BD_List*n = bd_cons( p , d , p->next ) ;
if ( n != NULL ) {
p->next->prev = n ;
p->next = n ;
}
}
// 双方向リストの指定場所 p の後ろのデータを消す処理は?
void bd_delete( struct BD_List* p ) {
struct BD_List* d = p->next ;
d->next->prev = p ;
p->next = d->next ;
free( d ) ;
}
// この手のリスト処理のプログラムでは、命令の順序が重要となる。
// コツとしては、修正したい箇所の遠くの部分を操作する処理から
// 書いていくと間違いが少ない。
番兵と双方向循環リスト
前述の bd_insert() だが、データの先頭にデータを挿入したい場合は、どう呼び出せば良いだろうか?
bd_insert() で、末尾にデータを挿入する処理は、正しく動くだろうか?
同じく、bd_delete() だが、データの先頭のデータを消したい場合は、どう呼び出せば良いだろうか?
また、データを消す場合、最後の1件のデータが消えて、データが0件になる場合、bd_delete() は正しく動くだろうか?
こういった問題が発生した場合、データが先頭・末尾で思ったように動かない時、0件になる場合に動かない時、特別処理でプログラムを書くことは、プログラムを読みづらくしてしまう。そこで、一般的には 循環リストの時にも紹介したが、番兵(Sentinel) を置くことが多い。
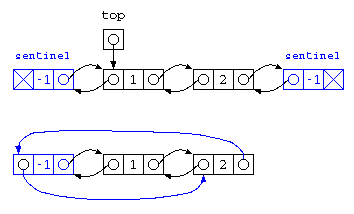
しかし、先頭用の番兵、末尾用の番兵を2つ用意するぐらいなら、先頭と末尾のデータを1つにまとめた方がムダがない。この場合上図のように末尾データが先頭データにつながる循環リストとなる。このような双方向リストでの循環した構造は、双方向循環リスト(bi-directional ring list)と呼ばれる。
deque(両端キュー)
この双方向循環リストを使うと、(1)先頭にデータを挿入(unshift)、(2)先頭のデータを取り出す(shift)、(3)末尾にデータを追加(push)、(4)末尾のデータを取り出す(pop)、といった処理が簡単に記述できる。この4つの処理を使うと、単純リスト構造で説明した、待ち行列(queue)やスタック(stack) が実現できる。この特徴を持つデータ構造は、先頭・末尾の両端を持つ待ち行列ということで、deque (double ended queue) とも呼ばれる。
理解確認
- 双方向リストとはどのようなデータ構造か図を示しながら説明せよ。
- 双方向リストの利点と欠点はなにか?
- 番兵を用いる利点を説明せよ。
- deque の機能と、それを実現するためのデータをリストを用いて実装するには、どうするか?
- 双方向リストが使われる処理の例としてどのようなものがあるか?
深さ優先探索と幅優先探索
2分探索木の説明で、深さ優先探索、幅優先探索の話をしたので、補足説明。
幅優先探索(breadth-first search)は、待ち行列を使って実装可能なことを示すサンプルコード。待ち行列は授業で説明したFIFOでは、データ件数0になる際の処理を手抜きで説明しているため、C++ の deque で記述。
深さ優先探索(deep-first search)は、スタックを使って実装可能なことを示すために、あえて再帰呼び出しを使わずに記述してみた。
#include <deque>
#include <algorithm>
int main() {
std::deque<struct Tree*> deq ;
struct Tree* p ;
// 幅優先探索(FIFOを使って)
deq.push_front( top ) ;
while( !deq.empty() ) {
// 待ち行列の最初を取り出す
p = deq.front() ;
deq.pop_front() ;
if ( p != NULL ) {
printf( "%d\n" , p->data ) ;
// 待ち行列に枝葉を追加
deq.push_back( p->left ) ;
deq.push_back( p->right ) ;
}
}
// 深さ優先探索(再帰呼び出しを使わずstack/LIFOで実装)
p = top ;
for( ;; ) {
// 分岐をpushしながら左下にまっしぐら
while( p != NULL ) {
deq.push_front( p ) ;
p = p->left ;
}
if ( deq.empty() )
break ;
// pushしておいた分岐点をpopして繰り返し
p = deq.front() ;
deq.pop_front() ;
printf( "%d\n" , p->data ) ;
p = p->right ;
}
return 0 ;
}
双方向リスト
最初に、前期期末試験で「メモリの番地の理解が怪しい」人が多かったので、その確認のための Forms による小テストを行う。
実施してみらた、各問題とも50%程度の正解率。ひとまず解説をしたうえで、同じような問題を今後も何度かやってみたいと思う。
リスト構造の利点と欠点
リストを使った集合演算のように、データを連ねたリストは、単純リストとか線形リストと呼ばれる。特徴はデータ数に応じてメモリを確保する点や、途中へのデータの挿入削除が得意な点があげられる。一方で、配列は想定最大データ件数で宣言してしまうと、実際のデータ数が少ない場合、メモリの無駄も発生する。しかし、想定件数と実データ件数がそれなりに一致していれば、無駄も必要最小限となる。リスト構造では、次のデータへのポインタを必要とすることから、常にポインタ分のメモリは、データにのみ注目すれば無駄となる。
例えば、整数型のデータを最大 MAX 件保存したいけど、実際は それ以下の、平均 N 件扱うとする。この時のメモリの使用量 M は、以下のようになるであろう。
| 配列の場合 | リスト構造の場合 |
(ただしヒープ管理用メモリ使用量は無視) |
シーケンシャルアクセス・ランダムアクセス
もう1つの欠点がシーケンシャルアクセスとなる。テープ上に記録された情報を読む場合、後ろのデータを読むには途中データを読み飛ばす必要があり、データ件数に比例したアクセス時間を要する。このような N番目 データ参照に、O(N)の時間を要するものは、シーケンシャルアクセスと呼ばれる。
一方、配列はどの場所であれ、一定時間でデータの参照が可能であり、これは ランダムアクセスと呼ばれる。N番目のアクセス時間がO(1)を要する。
このため、プログラム・エディタの文字データの管理などに単純リストを用いた場合、1つ前の行に移動するには、先頭から編集行までの移動で O(N) の時間がかかり、大量の行数の編集では、使いものにならない。ここで、シーケンシャルアクセスでも1つ前にもどるだけでも処理時間を改善してみよう。
単純リストから双方向リストへ
ここまで説明してきた単純リストは、次のデータへのポインタを持つ。ここで、1つ後ろのデータ(N番目からN+1番目)をアクセスするのは簡単だけど、1つ前のデータ(N-1番目)を参照しようと思ったら、先頭から(N-1)番目を辿るしかない。でも、これは O(N) の処理であり時間がかかる処理。
ではどうすればよいのか?
この場合、一つ前のデータの場所を覚えているポインタがあれば良い。

// 双方向リストの宣言
struct BD_List {
struct BD_List* prev ; // 1つ前のデータへのポインタ
int data ;
struct BD_List* next ; // 次のデータへのポインタ
} ;
このデータ構造は、双方向リスト(bi-directional list)と呼ばれる。では、簡単なプログラムを書いてみよう。双方向リストのデータを簡単に生成するための補助関数から書いてみる。
// リスト生成補助関数
struct BD_List* bd_cons( struct BD_List* p ,
int d ,
struct BD_List* n ) {
struct BD_List* ans ;
ans = (struct BD_List*)malloc(
sizeof( struct BD_List ) ) ;
if ( ans != NULL ) {
ans->prev = p ;
ans->data = d ;
ans->next = n ;
}
return ans ;
}
void main() {
struct BD_List* top ;
struct BD_List* p ;
// 順方向のポインタでリストを生成
top = bd_cons( NULL , 1 ,
bd_cons( NULL , 2 ,
bd_cons( NULL , 3 , NULL ) ) ) ;
// 逆方向のポインタを埋める
top->next->prev = top ;
top->next->next->prev = top->next ;
// リストを辿る処理
for( p = top ; p->next != NULL ; p = p->next )
printf( "%d\n" , p->data ) ;
for( ; p->prev != NULL ; p = p->prev )
printf( "%d\n" , p->data ) ;
}
双方向リストの関数作成
以上の説明で、双方向の基礎的なプログラムの意味が分かった所で、練習問題。
先のプログラムでは、1,2,3 を要素とするリストを、ナマで記述していた。実際には、どんなデータがくるか分からないし、指定したポインタ p の後ろに、データを1件挿入する処理 bd_insert( p , 値 ) , また、p の後ろのデータを消す処理 bd_delete( p ) を書いてみよう。

// 双方向リストの指定場所 p の後ろに、値 d を要素とするデータを挿入せよ。
void bd_insert( struct BD_List* p , int d ) {
struct BD_List*n = bd_cons( p , d , p->next ) ;
if ( n != NULL ) {
p->next->prev = n ;
p->next = n ;
}
}
// 双方向リストの指定場所 p の後ろのデータを消す処理は?
void bd_delete( struct BD_List* p ) {
struct BD_List* d = p->next ;
d->next->prev = p ;
p->next = d->next ;
free( d ) ;
}
// この手のリスト処理のプログラムでは、命令の順序が重要となる。
// コツとしては、修正したい箇所の遠くの部分を操作する処理から
// 書いていくと間違いが少ない。
番兵と双方向循環リスト
前述の bd_insert() だが、データの先頭にデータを挿入したい場合は、どう呼び出せば良いだろうか?
bd_insert() で、末尾にデータを挿入する処理は、正しく動くだろうか?
同じく、bd_delete() だが、データの先頭のデータを消したい場合は、どう呼び出せば良いだろうか?
また、データを消す場合、最後の1件のデータが消えて、データが0件になる場合、bd_delete() は正しく動くだろうか?
こういった問題が発生した場合、データが先頭・末尾で思ったように動かない時、0件になる場合に動かない時、特別処理でプログラムを書くことは、プログラムを読みづらくしてしまう。そこで、一般的には 循環リストの時にも紹介したが、番兵(Sentinel) を置くことが多い。

しかし、先頭用の番兵、末尾用の番兵を2つ用意するぐらいなら、循環リストにした方が便利となる。このような双方向リストでの循環した構造は、双方向循環リスト(bi-directional ring list)と呼ばれる。
deque(両端キュー)
この双方向循環リストを使うと、(1)先頭にデータを挿入(unshift)、(2)先頭のデータを取り出す(shift)、(3)末尾にデータを追加(push)、(4)末尾のデータを取り出す(pop)、といった処理が簡単に記述できる。この4つの処理を使うと、単純リスト構造で説明した、待ち行列(queue)やスタック(stack) が実現できる。この特徴を持つデータ構造は、先頭・末尾の両端を持つ待ち行列ということで、deque (double ended queue) とも呼ばれる。
理解確認
- 双方向リストとはどのようなデータ構造か図を示しながら説明せよ。
- 双方向リストの利点と欠点はなにか?
- 番兵を用いる利点を説明せよ。
- deque の機能と、それを実現するためのデータをリストを用いて実装するには、どうするか?
- 双方向リストが使われる処理の例としてどのようなものがあるか?
双方向リスト
リスト構造の利点と欠点
リストを使った集合演算のように、データを連ねたリストは、単純リストとか線形リストと呼ばれる。特徴はデータ数に応じてメモリを確保する点や、途中へのデータの挿入削除が得意な点があげられる。一方で、配列は想定最大データ件数で宣言してしまうと、実際のデータ数が少ない場合、メモリの無駄も発生する。しかし、想定件数と実データ件数がそれなりに一致していれば、無駄も必要最小限となる。リスト構造では、次のデータへのポインタを必要とすることから、常にポインタ分のメモリは、データにのみ注目すれば無駄となる。
シーケンシャルアクセス・ランダムアクセス
もう1つの欠点がシーケンシャルアクセスとなる。テープ上に記録された情報を読む場合、後ろのデータを読むには途中データを読み飛ばす必要があり、データ件数に比例したアクセス時間を要する。このような N番目 データ参照に、O(N)の時間を要するものは、シーケンシャルアクセスと呼ばれる。
一方、配列はどの場所であれ、一定時間でデータの参照が可能であり、これは ランダムアクセスと呼ばれる。N番目のアクセス時間がO(1)を要する。
このため、プログラム・エディタの文字データの管理などに単純リストを用いた場合、1つ前の行に移動するには、先頭から編集行までの移動で O(N) の時間がかかり、大量の行数の編集では、使いものにならない。ここで、シーケンシャルアクセスでも1つ前にもどるだけでも処理時間を改善してみよう。
単純リストから双方向リストへ
ここまで説明してきた単純リストは、次のデータへのポインタを持つ。ここで、1つ後ろのデータ(N番目からN+1番目)をアクセスするのは簡単だけど、1つ前のデータ(N-1番目)を参照しようと思ったら、先頭から(N-1)番目を辿るしかない。でも、これは O(N) の処理であり時間がかかる処理。
ではどうすればよいのか?
この場合、一つ前のデータの場所を覚えているポインタがあれば良い。

// 双方向リストの宣言
struct BD_List {
struct BD_List* prev ; // 1つ前のデータへのポインタ
int data ;
struct BD_List* next ; // 次のデータへのポインタ
} ;
このデータ構造は、双方向リスト(bi-directional list)と呼ばれる。では、簡単なプログラムを書いてみよう。双方向リストのデータを簡単に生成するための補助関数から書いてみる。
// リスト生成補助関数
struct BD_List* bd_cons( struct BD_List* p ,
int d ,
struct BD_List* n ) {
struct BD_List* ans ;
ans = (struct BD_List*)malloc(
sizeof( struct BD_List ) ) ;
if ( ans != NULL ) {
ans->prev = p ;
ans->data = d ;
ans->next = n ;
}
return ans ;
}
void main() {
struct BD_List* top ;
struct BD_List* p ;
// 順方向のポインタでリストを生成
top = bd_cons( NULL , 1 ,
bd_cons( NULL , 2 ,
bd_cons( NULL , 3 , NULL ) ) ) ;
// 逆方向のポインタを埋める
top->next->prev = top ;
top->next->next->prev = top->gt;next ;
// リストを辿る処理
for( p = top ; p->next != NULL ; p = p->next )
printf( "%d\n" , p->data ) ;
for( ; p->prev != NULL ; p = p->prev )
printf( "%d\n" , p->data ) ;
}
双方向リストの関数作成
以上の説明で、双方向の基礎的なプログラムの意味が分かった所で、練習問題。
先のプログラムでは、1,2,3 を要素とするリストを、ナマで記述していた。実際には、どんなデータがくるか分からないし、指定したポインタ p の後ろに、データを1件挿入する処理 bd_insert( p , 値 ) , また、p の後ろのデータを消す処理 bd_delete( p ) を書いてみよう。

// 双方向リストの指定場所 p の後ろに、値 d を要素とするデータを挿入せよ。
void bd_insert( struct BD_List* p , int d ) {
struct BD_List*n = bd_cons( p , d , p->next ) ;
if ( n != NULL ) {
p->next->prev = n ;
p->next = n ;
}
}
// 双方向リストの指定場所 p の後ろのデータを消す処理は?
void bd_delete( struct BD_List* p ) {
struct BD_List* d = p->next ;
d->next->prev = p ;
p->next = d->next ;
free( d ) ;
}
// この手のリスト処理のプログラムでは、命令の順序が重要となる。
// コツとしては、修正したい箇所の遠くの部分を操作する処理から
// 書いていくと間違いが少ない。
番兵と双方向循環リスト
前述の bd_insert() だが、データの先頭にデータを挿入したい場合は、どう呼び出せば良いだろうか?
bd_insert() で、末尾にデータを挿入する処理は、正しく動くだろうか?
同じく、bd_delete() だが、データの先頭のデータを消したい場合は、どう呼び出せば良いだろうか?
また、データを消す場合、最後の1件のデータが消えて、データが0件になる場合、bd_delete() は正しく動くだろうか?
こういった問題が発生した場合、データが先頭・末尾で思ったように動かない時、0件になる場合に動かない時、特別処理でプログラムを書くことは、プログラムを読みづらくしてしまう。そこで、一般的には 循環リストの時にも紹介したが、番兵(Sentinel) を置くことが多い。

しかし、先頭用の番兵、末尾用の番兵を2つ用意するぐらいなら、循環リストにした方が便利となる。このような双方向リストでの循環した構造は、双方向循環リスト(bi-directional ring list)と呼ばれる。
deque(両端キュー)
この双方向循環リストを使うと、(1)先頭にデータを挿入(unshift)、(2)先頭のデータを取り出す(shift)、(3)末尾にデータを追加(push)、(4)末尾のデータを取り出す(pop)、といった処理が簡単に記述できる。この4つの処理を使うと、単純リスト構造で説明した、待ち行列(queue)やスタック(stack) が実現できる。この特徴を持つデータ構造は、先頭・末尾の両端を持つ待ち行列ということで、deque (double ended queue) とも呼ばれる。
理解確認
- 双方向リストとはどのようなデータ構造か図を示しながら説明せよ。
- 双方向リストの利点と欠点はなにか?
- 番兵を用いる利点を説明せよ。
- deque の機能と、それを実現するためのデータをリストを用いて実装するには、どうするか?
- 双方向リストが使われる処理の例としてどのようなものがあるか?
双方向リスト
単純リストから双方向リストへ
ここまで説明してきた単純リストは、次のデータへのポインタを持つ。ここで、1つ後ろのデータ(N番目からN+1番目)をアクセスするのは簡単だけど、1つ前のデータ(N-1番目)を参照しようと思ったら、先頭から(N-1)番目を辿るしかない。でも、これは O(N) の処理であり時間がかかる処理。
ではどうすればよいのか?
この場合、一つ前のデータの場所を覚えているポインタがあれば良い。

// 双方向リストの宣言
struct BD_List {
struct BD_List* prev ; // 1つ前のデータへのポインタ
int data ;
struct BD_List* next ; // 次のデータへのポインタ
} ;
このデータ構造は、双方向リスト(bi-directional list)と呼ばれる。では、簡単なプログラムを書いてみよう。双方向リストのデータを簡単に生成するための補助関数から書いてみる。
// リスト生成補助関数
struct BD_List* bd_cons( struct BD_List* p ,
int d ,
struct BD_List* n ) {
struct BD_List* ans ;
ans = (struct BD_List*)malloc(
sizeof( struct BD_List ) ) ;
if ( ans != NULL ) {
ans->prev = p ;
ans->data = d ;
ans->next = n ;
}
return ans ;
}
void main() {
struct BD_List* top ;
struct BD_List* p ;
// 順方向のポインタでリストを生成
top = bd_cons( NULL , 1 ,
bd_cons( NULL , 2 ,
bd_cons( NULL , 3 , NULL ) ) ) ;
// 逆方向のポインタを埋める
top->next->prev = top ;
top->next->next->prev = top->gt;next ;
// リストを辿る処理
for( p = top ; p->next != NULL ; p = p->next )
printf( "%d\n" , p->data ) ;
for( ; p->prev != NULL ; p = p->prev )
printf( "%d\n" , p->data ) ;
}
双方向リストの関数作成
以上の説明で、双方向の基礎的なプログラムの意味が分かった所で、練習問題。
先のプログラムでは、1,2,3 を要素とするリストを、ナマで記述していた。実際には、どんなデータがくるか分からないし、指定したポインタ p の後ろに、データを1件挿入する処理 bd_insert( p , 値 ) , また、p の後ろのデータを消す処理 bd_delete( p ) を書いてみよう。

// 双方向リストの指定場所 p の後ろに、値 d を要素とするデータを挿入せよ。
void bd_insert( struct BD_List* p , int d ) {
struct BD_List*n = bd_cons( p , d , p->next ) ;
if ( n != NULL ) {
p->next->prev = n ;
p->next = n ;
}
}
// 双方向リストの指定場所 p の後ろのデータを消す処理は?
void bd_delete( struct BD_List* p ) {
struct BD_List* d = p->next ;
d->next->prev = p ;
p->next = d->next ;
free( d ) ;
}
// この手のリスト処理のプログラムでは、命令の順序が重要となる。
// コツとしては、修正したい箇所の遠くの部分を操作する処理から
// 書いていくと間違いが少ない。
番兵と双方向循環リスト
前述の bd_insert() だが、データの先頭にデータを挿入したい場合は、どう呼び出せば良いだろうか?
bd_insert() で、末尾にデータを挿入する処理は、正しく動くだろうか?
同じく、bd_delete() だが、データの先頭のデータを消したい場合は、どう呼び出せば良いだろうか?
また、データを消す場合、最後の1件のデータが消えて、データが0件になる場合、bd_delete() は正しく動くだろうか?
こういった問題が発生した場合、データが先頭・末尾で思ったように動かない時、0件になる場合に動かない時、特別処理でプログラムを書くことは、プログラムを読みづらくしてしまう。そこで、一般的には 循環リストの時にも紹介したが、番兵(Sentinel) を置くことが多い。

しかし、先頭用の番兵、末尾用の番兵を2つ用意するぐらいなら、循環リストにした方が便利となる。このような双方向リストでの循環した構造は、双方向循環リスト(bi-directional ring list)と呼ばれる。
この双方向循環リストを使うと、(1)先頭にデータを挿入(unshift)、(2)先頭のデータを取り出す(shift)、(3)末尾にデータを追加(push)、(4)末尾のデータを取り出す(pop)、といった処理が簡単に記述できる。この4つの処理を使うと、単純リスト構造で説明した、待ち行列(queue)やスタック(stack) が実現できる。この特徴を持つデータ構造は、先頭・末尾の両端を持つ待ち行列ということで、deque (double ended queue) とも呼ばれる。
理解確認
- 双方向リストとはどのようなデータ構造か図を示しながら説明せよ。
- 双方向リストの利点と欠点はなにか?
- 番兵を用いる利点を説明せよ。
- deque の機能と、それを実現するためのデータをリストを用いて実装するには、どうするか?
- 双方向リストが使われる処理の例としてどのようなものがあるか?